Язык чисел. Положительные и отрицательные числа

Понятие числа-основное в математике. Различие между «одно и много», по-видимому, относится к простейшим, доступным пониманию даже ребенка. Мальчик на берегу моря может взять один камешек, хотя видит много их. Взяв пригоршню камешков, он будет держать в руке более одного камешка, но гораздо меньше того, что видит. Чтобы установить точно, сколько у него камешков, мальчик может пересчитать их. Предположим, их 12. «Двенадцать»-название, данное этому числу камешков. Тем же свойством обладают все наборы из 12 предметов: 12 коров, 12 чаек, 12 энциклопедий и т.д.

Положительные и отрицательные числа. Такие целые числа, как 1, 5 и 212, называются положительными целыми числами. Люди пользовались ими задолго до того, как научились считать. В средние века индусы разработали понятие отрицательного числа, что позволило манипулировать при расчетах не только с наличными предметами, но и с долгами. Скажем, человек имеет пять (+ 5) овец, но он должен две (— 2) овцы, поэтому в действительности ему принадлежат только 5 — 2 = 3 овцы.

Покуда математические операции ограничены счетом, можно обойтись целыми числами. Но стоит перейти к измерениям, как выясняется, что длины и площади в природе не всегда выражаются целыми числами. Крестьянин может изготовить мерную линейку, взяв, например, за единицу длины собственную стопу. Измерив линейкой одно из своих животных, крестьянин обнаружит, что его длина 5 «стоп», а длина детеныша-только 2 «стопы». Другое животное может иметь в длину 3 1/2 «стопы», третье -2 1/3 «стопы». Так крестьянин откроет семейство чисел, называемых рациональными. Любое число, которое можно записать в виде дроби (отношения двух целых чисел), называется рациональным. Рациональные числа могут быть положительными и отрицательными. Все целые числа рациональны.

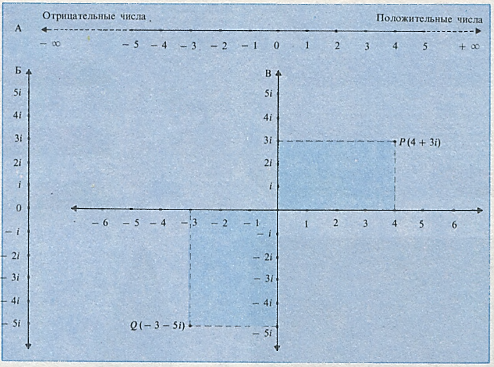
Существуют три типа чисел: вещественные, мнимые и комплексные. Вещественные числа (А) можно представить в виде точек на прямой, простирающейся от минус бесконечности до плюс бесконечности,-это все отрицательные и положительные числа. Мнимые числа (Б)-числа, кратные і (квадратному корню из — 1). Они также могут быть положительными и отрицательными. Комплексные числа (В) состоят из вещественной и мнимой частей. Их можно изобразить в виде точек на плоскости, находящихся на соответствующих расстояниях от вещественной и мнимой осей. Например, комплексное число Р равно 4 + Зі, a Q равно — 3 - 5і. Комплексные числа широко используются в науке.

В VI в. до н. э. греческие математики обнаружили, что квадрат с единичными сторонами имеет диагонали, длину которых невозможно измерить точно. Независимо от выбора единицы длины и того, на сколько мелких долей она будет разделена, длину диагонали не удается измерить точно и записать в виде дроби. Числовую систему пришлось расширить, чтобы включить в нее новый класс чисел, называемых иррациональными.

Сегодня мы обозначаем нулем (0) длину отрезка, в котором не укладывается ни одна сколь угодно малая доля единицы длины, но так было не всегда. Например, в римской числовой системе нуля не было. Его ввели около 600 г. до н. э. индийские математики, которые сформулировали правила для вычислений с нулем: при умножении на нуль любого числа произведение всегда равно нулю, от прибавления или вычитания нуля число не изменяется. Индийские математики установили также, что результат деления на нуль не может быть равен ни одному из чисел.

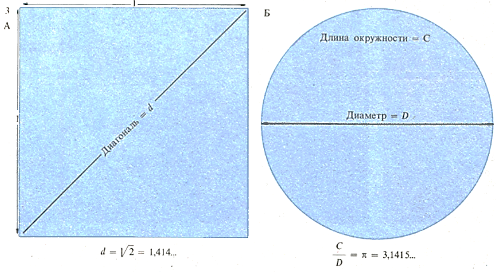
Иррациональное число нельзя представить в виде дроби, числитель и знаменатель которой- целые числа. Диагональ квадрата со стороной 1 (А) равна 1/2. Это - иррациональное число 1,414… (число знаков после запятой бесконечно). Другое иррациональное число-отношение длины окружности к ее диаметру (Б), которое принято обозначать π. Оно равно 3,1415 .... Грубым приближением к числу π служит дробь (рациональное число) 22/7, равная 3,1428.... Иррациональные числа были открыты древнегреческим математиком Пифагором.

Бесконечность и мнимые числа. Представление о бесконечно больших числах первым ввел древнегреческий математик Архимед (около 287-212 гг. до н. э.). Начав с наибольшего в греческой числовой системе числа-«мириада мириад» (100 млн.), он построил еще большие числа; затем, оценив число песчинок во Вселенной, показал, что оно меньше наибольшего из полученных им чисел.

Архимед доказал, что в числовой системе не существует верхнего предела. В отличие от нуля бесконечность не число. Каким бы большим ни было число, всегда найдется сколько угодно еще больших чисел. Бесконечность недостижима.

С нулем и бесконечностью люди получили полную числовую систему, которую можно изобразить в виде прямой, простирающейся от минус бесконечности до плюс бесконечности (каждая точка прямой соответствует какому-нибудь вещественному числу). Возведение в квадрат и извлечение квадратных корней поставило перед математиками новую проблему: чему равен квадратный корень из — 5? Сначала она казалась неразрешимой, так как не существует вещественного числа, квадрат которого был бы отрицательным? Но в XVI в. итальянские математики ввели «мнимую» единицу і, квадрат которой равен - 1. Числа, содержащие і, называются мнимыми.

Комплексные числа состоят из вещественной и мнимой частей, например 5 + Зі. Обращаться с ними можно так же, как с чисто вещественными числами. Комплексные числа используются при расчетах электрических цепей.

Современная система счисления заимствована у арабов, которые переняли ее идеи у индусов. В ней существенно положение цифры. Все числа можно записать при помощи цифр от 0 до 9. Это-система счисления с основанием 10 (десятичная система), введенная в Европе около 1120 г. Аделардом из Бата и распространившаяся к 1600 г. почти повсюду.

Немало различных числовых систем было создано людьми. В древнейших из них, например в системе, принятой в Египте, число 1 обозначали чертой. Числа 2, 3, ..., 9 записывали, повторяя символ единицы. У римлян и народов майя был специальный символ для обозначения числа 5. Арабы и китайцы каждое число записывали особым знаком, хотя целые числа от 1 до 3 обозначали просто черточками.

Что такое основание системы счисления. Основание - это число цифр в системе счисления. Положение цифр существенно: например, в числе 333 первая цифра 3 означает 300 (3 сотни), вторая-30 (3 десятка) и третья-3 единицы. Но в принципе основанием может быть любое число. Например, современные ЭВМ считают в двоичной системе (с основанием 2), так как состояния «сигнал» - «нет сигнала» легко представить лишь двумя цифрами 1 и 0.

Большие числа записывать трудно. Даже в англоязычных странах, например в Англии и США, их называют по-разному. В науке такие числа принято записывать в виде степеней десятки.

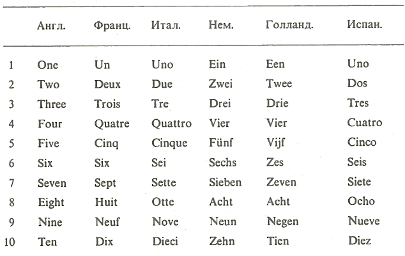
Названия чисел в различных европейских языках обнаруживают общее происхождение. Все европейские страны пользуются единой числовой системой, в основу которой положены древние арабские числа.