Грамматика чисел. Основные правила арифметики

В повседневной жизни люди используют арифметику так часто, что даже не задумываются об этом. Когда домашняя хозяйка покупает что-нибудь и подсчитывает сдачу у кассы, она пользуется понятиями сложения и равенства, которые возникли, когда люди стали торговать.

Основные правила арифметики. Четыре основных арифметических действия-сложение, вычитание, умножение и деление. Они подчиняются определенным законам, большинство которых не выходит за рамки обычного здравого смысла. Перестановочный закон, справедливый для сложения и умножения, утверждает, что, например, сумма (7 + + 2) равна сумме (2 + 7), т.е. сумма не зависит от порядка слагаемых. Аналогично для умножения: 4 х 3 = 3 х 4, или в общем случае а х b = b х а.

Сочетательный закон есть более общая форма перестановочного. Он гласит, что при сложении или умножении нескольких чисел результат не зависит от порядка слагаемых или сомножителей. В общем виде это можно записать так: {а + b) + с = а + (b + с) или (а х b) х с = а х (b х с).

Распределительный закон утверждает, что если сложить два числа и сумму умножить на третье число, то получится тот же результат, как если бы мы сначала умножили каждое из двух первых чисел на третье, а затем сложили полученные произведения. Этот закон легче понять, записав его в общем виде: (а + b) х с = (а х с) + (b х с), например (5 + 7) х 3 = (5 х 3) + (7 х 3) = 36.

Умножение эквивалентно многократно повторенному сложению. Например, (7 х 5)-сокращенная запись сложения (7 + 7 + 7 + 7 + 7). Таблица умножения нужна нам потому, что пользоваться ею быстрее, чем суммировать столбцы цифр. Электронные вычислительные машины и микрокалькуляторы, обладающие высокими быстродействием и точностью, не производят умножения-они необычайно быстро многократно повторяют операцию сложения.

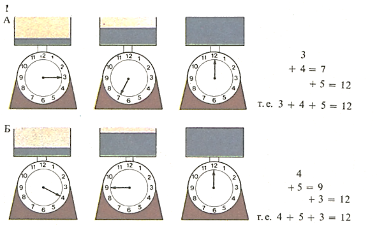
Сложение подчиняется сочетательному закону, т. е. результат нескольких операций сложения не зависит от порядка, в котором они производятся. На рисунках показано взвешивание на пружинных весах трех предметов: сначала (А) они ставятся на чашу весов в порядке возрастания массы (3, 4 и 5), а затем (Б)- в другом порядке (4, и 3). Общая масса в обоих случаях оказывается одинаковой (12)

Вычитание-операция, обратная сложению, а деление, операцию, обратную умножению, можно рассматривать как многократно повторенное вычитание. Именно так, по существу, выполняется «деление углом», при этом, вычитая одно число из другого, иногда невозможно получить нуль: обычно «что-нибудь» остается. Это «что-нибудь» называется остатком. Например, при делении 380 на 70 получается 5 и 30 в остатке.

Квадраты и квадратные корни. При возведении числа в квадрат оно умножается само на себя (площадь квадрата равна длине его стороны, умноженной на себя): число 3 в квадрате (З²) равно 9. Операция, обратная возведению в квадрат, называется извлечением квадратного корня: какое число при умножении на себя даст заданное число? При возведении в квадрат целого числа результат также оказывается целым. Но квадратный корень из целого числа не обязательно целое число. Пифагор и его последователи установили, что не всякое число, квадрат которого равен целому числу, является рациональным (представленным в виде отношения двух целых чисел). Квадратный корень из 4 равен 2 (оба числа целые), но квадратный корень из 2 заключен между 1,4142 и 1,4143, т.е. не представим в виде рационального числа и называется иррациональным числом.

Дроби, пропорции и отношения. Три седьмых мы записываем в виде 3/7, что означает 3, деленное на 7, и называется дробью. Число под чертой-знаменатель; он показывает, на сколько частей «разбита» единица. Число над чертой-числитель; он показывает, сколько таких частей взято. Если две рейки имеют в длину З и 7 м, то их длины относятся как 3:7, т. е. короткая рейка составляет 3/7 от длинной.

Существуют два типа дробей: правильные и неправильные. У правильных дробей числитель меньше знаменателя 3/7, 7/8, 29/54; у неправильных - числитель больше знаменателя 5/4, 22/7. Обычно их упрощают, деля числитель на знаменатель и записывая остаток в виде правильной дроби 5/4 = 1 ¼, 22/7 = З 1/7.

Арифметические действия применимы и к дробям, но при этом необходимо знать определенные правила. Умножение дробей производится просто: числитель умножается на числитель, знаменатель-на знаменатель, а результат записывается в виде новой дроби: 2/3 х 7/11 = 14/33. Чтобы разделить на дробь, нужно умножить на перевернутую дробь: 2/3 :7/11 = 2/3 * 11/7 = 22/21 = 1 1/21.

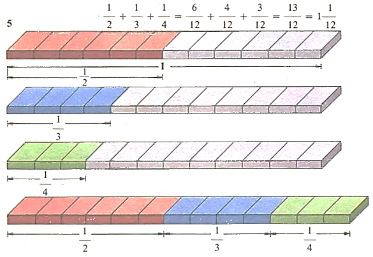
При сложении дробей их нужно привести к общему знаменателю. Например, чтобы найти сумму дробей 1/2, 1/3, 1/4, их нужно выразить через двенадцатые доли единицы (наименьший общий знаменатель здесь равен 12): 6/12, 4/12 И 3/12. Их сумма равна неправильной дроби 13/12, которую можно записать как 1 1/12 - Этот пример позволяет понять, почему ничто нельзя разделить на три доли 1/2, 1/3, И 1/4: сумма «долей» была бы больше целого

Сложение и вычитание дробей-более сложные операции. Чтобы выполнить их, дроби нужно привести к общему знаменателю. Для простоты выбирают наименьший общий знаменатель. Затем производят сложение или вычитание числителей, результат записывают в виде дроби с наименьшим общим знаменателем и в случае необходимости упрощают.

Десятичные дроби-особый способ записи дробей со знаменателями, равными степеням числа 10; целую часть числа от дробной отделяет запятая. Каждую дробь можно представить в виде суммы последовательности сотых, тысячных и т.д., т. е. записать в виде десятичной дроби.