Измерения и размерности. Приписывание чисел реальным объектам

Четырем студентам - химику, физику, математику и филологу-дали по барометру и попросили измерить высоту колокольни. Химик знал о газах все. Он измерил атмосферное давление на верхушке и у подножия колокольни и по едва ощутимой разнице заключил, что высота колокольни от 0 до 60 м. Физик обошелся с дорогим прибором весьма небрежно: сбросил его с верхушки колокольни и, измерив время падения, нашел, что высота колокольни составляет 27-33 м. Математик, сравнив длину теней, отбрасываемых колокольней и барометром, оценил высоту в 30-30,5 м. Филолог продал свой барометр и, угостив на вырученные деньги церковного сторожа, узнал, что высота колокольни точно равна 30,4 м.

Приписывание чисел реальным объектам. Эта шутливая история показывает, что есть немало способов «приписать числа реальным объектам», которые дают различные результаты. Но в наши дни очень часто требуются точные вычисления, и, чтобы обеспечить однозначность измерений, во всем мире используют единые эталоны длины, времени, массы и напряжения. На крупных предприятиях имеются приборы для измерения длины, калиброванные по эталонам, которые в свою очередь сверены с национальной копией эталона метра. Благодаря этому изготовленная в Японии шестерня для коробки передач в точности подходит к валу двигателя, сделанного на 5 лет раньше в Западной Германии.

За практикой измерения стоит теория. Существуют физическая теория измерений и такие математические теории, как анализ размерностей. Последний выражает все «размерности» измеряемых величин через основные: длину [L], массу [М] и время [Т]. Например, площадь (квадратные метры и т.д.) имеет размерность [L²], размерность объема (кубические метры и т.д.) равна [L³]. Если утверждается, будто объем параболического сосуда равен πH²/8D, где Н- высота, a D- диаметр основания, то без вычислений ясно, что формула не верна, поскольку соответствующая ей размерность равна [L²/L] = [L]. Такая формула могла бы выражать длину, но никак не объем. (Правильная формула πH²D/8.)

Аналогично период колебаний маятника t может зависеть от его длины L, массы груза т и ускорения свободного падения g, поэтому любая формула для t, основанная на некотором соотношении между L, m и g, должна иметь раз мерность времени. Ускорение измеряется в метрах в секунду за секунду, его размерность равна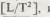

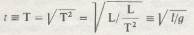(знак = здесь означает «эквивалентно»).

Окончательно формула имеет вид 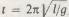(множитель 2π нельзя вывести из соображений размерности). Анализ размерностей помогает при проверке правильности вычислений, но физические законы невозможно вывести из одних лишь математических принципов. Только эксперимент может подтвердить, что период колебаний маятника не зависит от его массы.

Если длина измерена в метрах, а ускорение в метрах в секунду за секунду, то период получится в секундах. «Самосогласованные» системы единиц, например СИ (Международная система единиц, используемая во всем мире), гарантируют получение ответа в правильных единицах. Например, умножив скорость поршня на его площадь и давление, мы получим развиваемую им мощность, причем система СИ (м/с, м² и Н/м²) дает ее значение в ваттах (Вт). Широко используются также системы СГС (сантиметр-грамм-секунда) и МКС (метр — килограмм - секунда).

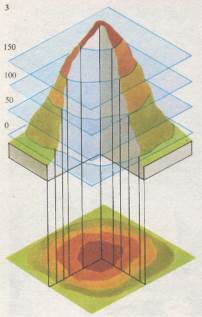
Изображения трехмерных объектов на плоскости получают с помощью так называемых горизонталей. На этом рисунке контуры горизонтальных сечений холма, проведенных на высотах 50, 100 и 150 м, спроектированы на карту холма. Такое изображение позволяет «ощутить» крутизну склонов, хотя оно довольно грубо. О крутизне склонов можно судить по густоте линий равной высоты. «Кольца Ньютона» и другие интерференционные картины (см. рис. 2) могут служить примером «тонких» контурных карт, по которым с помощью специальных методов можно наблюдать малейшие деформации напряженных поверхностей.

Моделирование. Если 10-метровая модель травинки была бы «сделана» из того же материала, что и настоящая травинка, то она не выдержала бы собственной тяжести и сломалась. Блоха величиной со слона не могла бы стоять, не говоря уже о том, чтобы прыгать. Дело в том, что масса и объем тела возрастают, как куб его высоты, тогда как прочность возрастает лишь пропорционально ее квадрату. При изменении линейных размеров объекта изменяются и его свойства, поэтому так трудно, например, пересчитать силу сопротивления, измеренную на модели самолета в аэродинамической трубе, на реальный объект. Один из выходов состоит в том, чтобы выразить параметры через безразмерные отношения или величины. В гидро- и аэродинамике такой величиной, например, является число Рейнольдса: 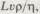, где L- длина (сечения крыла), ʋ-скорость газа, p-его плотность, ɳ-вязкость. Это отношение-безразмерное число, оно имеет одно и то же значение в любой системе единиц.

Термограмма показывает распределение температуры на коже лица человека. Термография позволяет врачу определять степень повреждения кожи при ожогах и служит для диагностики таких заболеваний, как рак груди. Инфракрасная камера имеет сканирующее устройство с вращающейся призмой, которое определяет распределение температуры вдоль узкой полоски изображения. Результирующий сигнал усиливается и подается на экран цветного телевизора. Голубые цвета соответствуют низким температурам, «покраснение» означает повышение температуры. Термография помогает проектировать жилые здания с минимальными потерями тепла.

Безразмерные отношения. Важное значение имеют безразмерные отношения, не зависящие от выбора единиц. Например, отношение интенсивностей электрического и гравитационного взаимодействий между протоном и электроном равно 10⁴⁰. Примерно такую же величину имеет отношение диаметра известной части Вселенной к диаметру протона или отношение возраста Вселенной ко времени, за которое свет проходит расстояние, равное диаметру протона. Квадрат числа 10³⁹- число 10⁷⁸-приблизительно равен числу частиц в известной части Вселенной. Некоторые космологи пытаются разгадать «таинственный смысл» этого отношения.