Каким образом представляются числа?

В десятичной системе счисления используется 10 значащих цифр — от 0 до 9. Они составляют основание (или базу) десятичной системы счисления. В десятичной системе счисления числа принято располагать справа налево, когда первая цифра представляет разряд единиц (100), вторая цифра представляет разряд десятков (101), третья цифра — разряд сотен (102) и т.д. При переходе к более старшему разряду значение числа возрастает, при этом увеличение кратно числу 10 в степени, показатель которой равняется числу разрядных переходов.

В десятичной системе счисления при переходе справа налево от одного разряда к более высокому значение разрядной цифры возрастает, увеличение равно числу 10 в степени, показатель которой равен количеству разрядных переходов. В двоичной, или бинарной, системе счисления при переходе от одного разряда к другому, более высокому, значение цифры возрастает, увеличение равно числу 2 в степени, показатель которой равен количеству разрядных переходов.

Бинарная, или двоичная, система счисления в качестве базы имеет число 2. В подавляющем большинстве случаев числа располагаются справа налево, точно так же, как и в десятичной системе счисления. Самый правый разряд, d0, образует разряд единиц (20), второй разряд, d1, составляет разряд двоек (21), третий разряд, d2, образует разряд четверок (22), четвертый разряд составляет разряд восьмерок (23) и т.д. В каждом более старшем разряде значение цифры возрастает, увеличение пропорционально числу 2 в соответствующей степени. В табл. 6.1 приводится сравнение двух систем счисления.

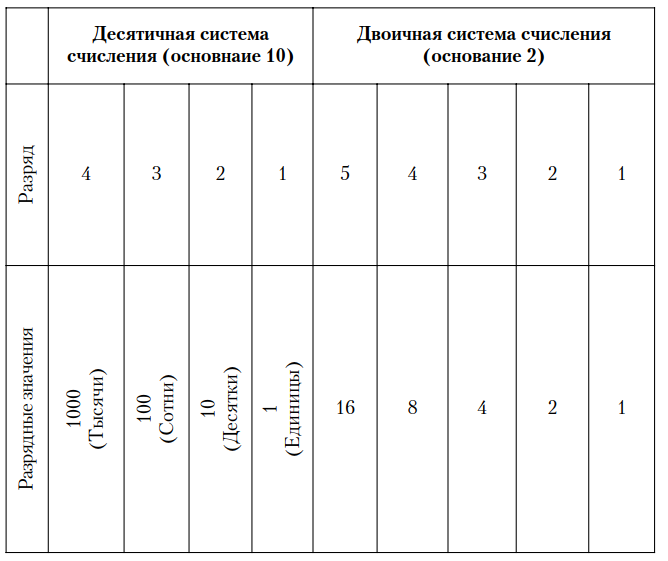
Таблица 6.1. Сравнение значений чисел в зависимости от занимаемого разряда

Для того чтобы использовать эти разрядные значения для кода, представленного на рис. 6.3, необходимо взять значения в тех разрядах, где имеются единицы; последующее складывание этих значений позволяет получить эквивалентное число в десятичной системе счисления. Например, преобразование двоичного кода 011 в десятичное число выполняется следующим образом:

(1*d0) + (1*d1) + (0*d2) = (1*1) + (1*2) + (0*4) =1 + 2 + 0 = 3.

Представление информации с использованием двоичных кодов. В случаях когда символы двоичного кода используются для отображения или представления информации вне зависимости от того, будут они обрабатываться или формироваться последовательно или параллельно, процесс передачи информации может осуществляться несколькими различными способами. Первый путь заключается в использовании законченных групп, образованных отдельными битами.

Для того чтобы отобразить информационные данные, биты могут быть сгруппированы несколькими различными способами. В одном из способов каждая 8-битовая группа используется для того, чтобы отобразить число или символ. Такая группа из 8 битов получила название байта.

На рис. 6.1а в качестве иллюстрации приводится восьмиразрядная (или 8-битовая) группа, являющаяся общепринятым способом организации (группирования) битов как в системах телефонной связи, так и в различных цифровых системах. Все биты, образующие данную группу, служат для однозначного распознавания информации. 8-битовая группа образует уникальный код, позволяющий распознавать состояния информации, которая была представлена в цифровой форме. Биты в каждой 8-битовой группе, как это явствует из рис. 6.1а, пронумерованы, начиная с d0 и кончая d7, при этом бит, расположенный под номером d0, называется самым младшим разрядным битом (или битом самого младшего двоичного разряда, LSB), а бит d7 — самым старшим значащим разрядным битом (битом самого старшего двоичного разряда, MSB).

При ином подходе какому-то конкретному биту предписывается функция указывать какое-нибудь особое состояние либо какую-нибудь возможность.

Как дополнение к использованию в качестве кода законченных битовых групп часто используются особые индивидуальные биты, находящиеся внутри группы, которые предназначены для управления особыми функциями либо для обозначения особого состояния. Наиболее типичным примером из области цифровой телефонной связи является установление (назначение) для одного из битов в группе состояния, которое бы однозначно указывало, лежит ли трубка телефонного аппарата на рычагах или она снята с них. Пример, приведенный на рис. 6.1а, наглядно демонстрирует такой подход.

Бит d7 из 8-битовой группы используется для того, чтобы характеризовать (указывать) состояние абонентского телефонного аппарата. Когда телефонная трубка снята с рычагов, биту d7 соответствует логический сигнал высокого уровня, или равный логической 1, когда же телефонная трубка лежит на рычагах, биту d7 соответствует логический сигнал низкого уровня, или равный логическому 0.

Следовательно, для ситуации, изображенной на рис. 6.1а, когда поступают биты, входящие в первую 8-битовую группу (случай последовательного метода обработки сигнала), биту d7 соответствует сигнал, равный логической 1, и система связи распознает, что телефонная трубка поднята с рычагов. Когда поступает вторая 8-битовая группа, биту d7 соответствует сигнал, равный логическому 0, поэтому будет определено состояние телефона, при котором телефонная трубка лежит на рычагах. Другие биты, находящиеся на иных позициях (в других разрядах), могут использоваться подобным же образом для идентификации сигналов управления и контроля.

В третьем методе используется прием подразделения группы битов на подгруппы, при этом каждая подгруппа представляет символ или букву в группе символов.

Третий прием при передаче информации заключается в использовании подгруппы битов. В качестве примера следует предположить, что код, образованной 8-битовой группой, разбит на подгруппы следующим образом:

010 1100 1

А В С

При этом способе три первых бита кода, подгруппа А, могут быть использованы для идентификации одного из восьми различных региональных центров связи. Следующие четыре бита, образующие подгруппу В, могут использоваться для совершенно иных целей, например для идентификации одной из 16 магистральных линий. Последние биты, образующие подгруппу С, могут опять быть использованы для идентификации положения телефонной трубки (поднята ли она с рычагов или же лежит на рычагах).