Как найти неизвестную величину: алгебра

В арифметике различные величины (длина, площадь и т.д.) выражаются числами (с указанием соответствующих единиц). Но в некоторых математических задачах число (неизвестную величину) требуется найти. Если сумма двух слагаемых равна 10 и одно из них равно 6, то чему равно другое? Ответ прост: 4, но метод формализации решения является основным методом алгебры.

Чтобы решить данную задачу алгебраически, обозначим неизвестную величину через х. Тогда 6 + х = 10 (алгебраическое уравнение). Вычитая из правой и левой частей уравнения по 6, получаем х = 10 — 6 = 4. Итак, введя неизвестное х, мы решили задачу. Использование буквенных символов вместо чисел и есть основной метод алгебры.

Греческие и арабские математики. Греческие математики, например Диофант (около III в.), использовали в уравнениях буквенные обозначения. Но слово «алгебра» произошло от арабского «аль-джебр», что означает «восстановление кости» (после перелома). Это слово входило в название небольшого сочинения арабского математика Аль-Хорезми. К XVI в. математические задачи были полностью переведены на алгебраический язык-сначала во Франции (Франсуа Виет, 1540-1603). По традиции, установленной французским математиком Рене Декартом (1596-1650), последними буквами латинского алфавита принято обозначать неизвестные, а первыми-известные величины.

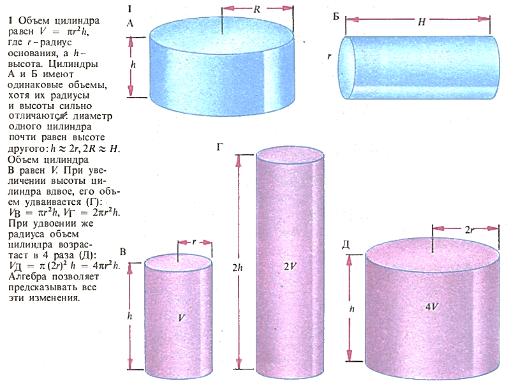
Алгебраические уравнения и формулы. Алгебраические уравнения широко применяются в различных науках, особенно в математике и физике. Например, объем цилиндра определяется по формуле V = πr²h, где Ѵ-объем, г-радиус и h-высота цилиндра. Формула представляет собой сокращенную запись выражения «объем цилиндра равен произведению площади основания на высоту».

Над алгебраическими уравнениями и формулами можно производить действия по определенным правилам. «Изменив» неизвестную в формуле объема цилиндра, мы можем, зная объем, вычислить радиус или высоту цилиндра, например . Эти формулы универсальны: они применимы ко всем цилиндрам независимо от того, высокие они и узкие или короткие и широкие. Аналогичные формулы существуют для площадей и объемов всех наиболее распространенных геометрических фигур.

Многие алгебраические задачи содержат более одной неизвестной. Предположим, требуется найти два положительных числа, произведение которых равно 15, а разность 2. Обозначим их х и у. Тогда информацию о произведении можно записать в виде х у = 15. Это уравнение допускает много решений: 1 и 15, 3 и 5, 2 и 7,5 и т.д. Запишем теперь информацию о разности чисел: у — х = 2, или у = х + 2. Подставляя правую часть этого уравнения вместо у в первое уравнение, получаем х(х + 2) = 15, или х² + 2х — 15 = 0.

Новое (третье) уравнение содержит только одно неизвестное х. Единственное положительное число, удовлетворяющее этому уравнению, равно 3 (при х = 3 уравнение превращается в тождество 9 + 6 — 15 = 0). Чтобы найти у, подставим значение х в любое из двух исходных уравнений. Из первого находим у = 15/х = 15/3 = 5, из второго у = х + 2 = 3 + 2 = 5. Итак, ответ получен: 3 и 5. На языке алгебры можно сказать, что мы решили систему из двух уравнений.

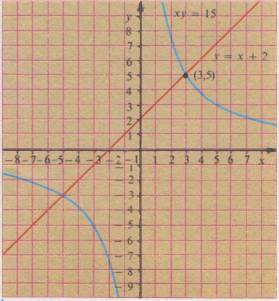
Если точки пространства задавать их расстояниями от осей х и у, то алгебраические уравнения приобретают новый смысл. Например, уравнение х*у = 15 описывает кривую, для всех точек которой произведение расстояния от оси х на расстояние от оси у равно 15. Уравнение у = х + 2 описывает прямую, координаты всех точек которой удовлетворяют этому уравнению.

Начертив эти кривые (в математике даже прямую считают «кривой»), мы увидим, что они пересекаются в точке, отстоящей на 3 единицы от оси х и на 5-от оси у. Такую точку принято обозначать (3,5). Графический метод решения уравнений дает в точности тот же результат, что и чисто алгебраический. Из графика также видно, что кривые пересекаются и в точке х = — 3, у = — 5. Однако это решение не удовлетворяет условиям задачи (требовалось найти два положительных числа).

Представлением алгебраических уравнений в виде кривых на плоскости с осями координат занимается аналитическая геометрия - область математики, в которой алгебра тесно переплетается с геометрией.

Алгебра позволяет решить многие головоломки и парадоксы. Всякое трехзначное число, у которого средняя цифра равна сумме двух крайних цифр, делится на 11. Почему? Алгебра позволяет без труда решить эту задачу.

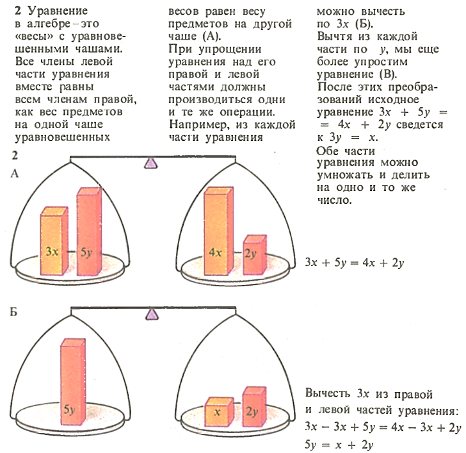
Алгебраическое «равновесие». Приведенные примеры показывают, как легко справляется алгебра с решением задач, в особенности с преобразованием уравнений. Однако при этом необходимо соблюдать некоторые правила. Если в уравнение входят два неизвестных х и у, то его можно упростить, перенеся все члены с x в одну часть уравнения, а члены с у-в другую. Достичь этого можно, прибавляя к обеим частям уравнения или вычитая из них равные величины.

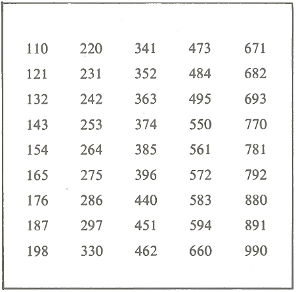
Трехзначные числа в этой таблице обладают двумя общими свойствами: их средняя цифра равна сумме крайних и все они делятся на 11. Если х-первая, у-последняя цифра, то средняя цифра равна х + у, а все число 100х + 10 (х + у) + у, а после упрощения и разложения на множители: 11 (10х + у). Такова общая формула всех чисел таблицы.