Математика и цивилизация. Первые математики

Математика в наши дни находит все более широкое применение в науке, технике, изобразительном искусстве, музыке, архитектуре, экономике, социологии, спорте, т. е. почти во всех областях человеческой деятельности. На протяжении всей истории своего развития математика не только отражала успехи цивилизации, но и немало способствовала им.

Алгебра, геометрия и математический анализ. В математике можно выделить три крупные области. Составление и комбинирование множеств из различных объектов привели к понятиям числа, счета и алгебры. Необходимость измерения времени и пространства способствовала возникновению геометрии, астрономии и хронологии. Развитие идей непрерывности и предела в XVII в. завершилось разработкой методов математического анализа и дифференциального и интегрального исчислений. Эти три обширных раздела математики значительно перекрываются, часто используя понятия друг у друга. Так, существуют алгебра множеств, векторная алгебра, алгебраическая геометрия.

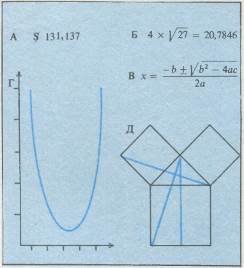
Математика создала свой собственный «язык». Числа представляют собой сокращенную форму записи слов и (вместе с единицами измерений) позволяют выразить величины и результаты измерений (А). Другие математические знаки служат для записи операций, например умножения и извлечения корня (Б).

В алгебре буквы часто обозначают величины, не имеющие определенных числовых значений (В). Алгебраические функции можно изображать в виде «графиков» (Г). Пифагор разработал собственные обозначения для геометрических фигур (Д)

Все, что создано природой или руками человека, обладает структурой, т. е. состоит из элементов, между которыми существуют определенные связи. Кристалл минерала, растение, космический корабль и политическая система обладают структурой, которую можно исследовать математическими средствами. Математика-продукт особого мыслительного процесса - абстракции, изучение реальной физической структуры она заменяет исследованием ее абстрактной модели. Сила математики становится особенно ощутимой, когда абстрактные понятия, например понятия числа и пространства, удается представить в виде алгебраических, геометрических или графических символов.

Математическое рассуждение - это извлечение следствий по определенным правилам из исходных математических истин. Однако, как показывает история, математика - это также область творческой деятельности с невиданными взлетами интуиции и воображения. Первым стимулом творческой активности математика обычно является стремление решить проблемы, стоящие перед обществом, но мотивом может служить и чисто «спортивный интерес».

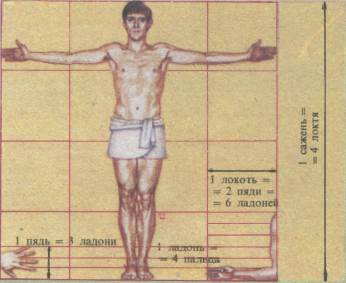
Человек, по-видимому, начал считать на пальцах и измерял различные предметы, сравнивая их с частями своего тела. «Телесные» единицы длины применяются кое-где и поныне. «Пядь» (около 10 см) до сих пор служит стандартной единицей при измерении роста лошадей, а в США и Великобритании в качестве единицы длины используется «ступня»-фут (30,5 см). В настоящее время наиболее распространена метрическая система мер.

Первые математики. Все примитивные цивилизации выработали понятия числа и меры, как только торговля вышла за рамки товарообмена. Почти 6 тыс. лет назад шумеры пользовались системой счисления с основанием 10 (десятичная система) и с основанием 60 (шестидесятиричная система). Последняя сохранилась и поныне в измерении углов и времени, напоминая нам о систематических наблюдениях вавилонских жрецов за движением Солнца, Луны и других планет и их влиянием на человека.

Накопленные знания помогали решать основные проблемы сельского хозяйства и организации общества. Разливы рек в Вавилоне и Египте требовали периодического восстановления границ земельных наделов, и землемерные работы способствовали зарождению геометрии. Политические, экономические и религиозные потребности в сооружении дворцов, судов, храмов, гробниц стимулировали дальнейшее развитие геометрии. В то же время астрономия устанавливала дни общественных и религиозных празднеств и тем самым служила интересам правящей касты жрецов.

Древние греки превратили математику в науку с незыблемыми выводами, подведя под математические рассуждения логический фундамент. Это позволило выводить из исходных посылок далеко не очевидные утверждения. «Начала» Евклида, созданные около 300 г. до н. э., стали образцом этого подхода и предопределили «геометрическое мышление» на 2 тыс. лет. Древние греки видели красоту в числе и форме, их преклонение перед «золотым сечением» наглядно проявилось в изобразительном искусстве и архитектуре, нашло отражение в архитектуре последующих времен (Собор Парижской богоматери, архитектура Ле Корбюзье, здание ООН в Нью- Йорке).

Древнегреческие математики распространили логическое мышление на искусство, установив математические соотношения в музыке, живописи и скульптуре. Особой привлекательностью для них обладало «золотое сечение» (примерно 1,618). Оно воплощено в пропорциях Парфенона (построенного в 447-438 гг. до н. э.).

Каждая цивилизация нуждалась в своей системе единиц измерения, и каждый новый метод заимствовал идеи у предшествующих. По мере распространения цивилизаций расширялась торговля и усиливалась потребность в единой системе измерения. Все ранние системы единиц строились по принципу удобства: так, длина измерялась в частях человеческого тела (пядях, локтях); площадь - работоспособностью скота, вес - камнями, объем - бурдюками. В 1791 г. во Франции была предложена метрическая система, основанная на метре - одной десятимиллионной четверти длины земного меридиана, вычисленной на основании геодезических измерений. Международная торговля заставила большинство стран западного мира принять метрическую систему измерений.

Отношения Фибоначчи образуют последовательность 1/1, 2/1, 3/2, 5/3, 8/5, 13/8 И Т. Д„ стремясь к золотому сечению. Числители и знаменатели дробей, начиная с третьей, образуются сложением соответственно числителей и знаменателей двух предыдущих. Отношения Фибоначчи встречаются в природе: расстояния и углы между черенками соседних листьев относятся примерно как 5/3.

Наследие чисел. Математика напоминает живой организм, развитие которого зависит от окружающей красавицу математику, но затем она на долгие годы впала в сон. Римляне использовали наследие своих предшественников, однако не решили ни одной новой проблемы. Существенных успехов в математике не было вплоть до XVI в. В наше время мир изменяется неслыханными ранее темпами. Это находит отражение и в развитии новых отраслей математики и ее приложений к решению научных, технических, производственных и экономических проблем.

Все на Земле-от атомов в кристаллах до листьев на дереве состоит из отдельных элементов. Математики пытаются установить соответствия между ними.