Как математики создали язык алгебры

Известно, что при решении задачи самое главное — осмыслить содержание задачи и выразить его на языке алгебры, т. е. записать условие задачи посредством символов — математических знаков.

Так, задачу, которая рассказывает о жизни Диофанта, можно перевести на язык алгебры следующим образом:

Все годы жизни Диофанта х лет,

Диофант провел шестую часть своей жизни в детстве -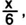

двенадцатую — в юности -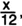

после седьмой части, проведенной в бездетном супружестве, и еще 5 лет у него родился сын -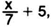

умерший по достижении половины числа лет жизни отца -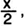

после чего Диофант прожил только 4 года – 4.

Сложив числа лет жизни Диофанта, выраженные иносказательно, получим х, т. е. составим уравнение: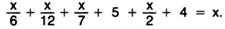

Решив это уравнение, найдем х=84. Диофант прожил 84 года. Это все, что нам известно о жизни замечательного ученого.

Диофант в своей «Арифметике» дает понятие об алгебраическом уравнении, записанном символами, однако очень далекими от современных. Путь к современному языку в математике — путь постепенного изобретения, преобразования и развития символов, начиная от египтян и вавилонян, был очень долгим.

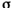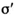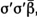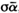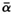Диофант обозначал неизвестное, которое он называл аритмос(число), греческой буквой (сигма), коэффициент при неизвестном ставил после неизвестного, а букву писал со штрихом и ее повторял. Неизвестное называл множеством. Например, 2х он записывал где ß означает 2, х выражал где = 1.

Квадрат неизвестного (х²) Диофант называл дюнамис и обозначал 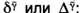х³ он записывал первой буквой слова кюбос 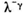(каппа). Известное число — знаком 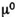— начальной буквой слова монас, что означает «один». В его записях 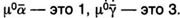Знак сложения он не писал - слагаемые он записывал рядом одно с другим, что и означало сумму.

Иногда он заменял символы их сокращенными названиями. Так, в его рукописи встречается замена неизвестного слогом ар, от слова аритмос — «число». Начало слова изос (равные) заменено ис или і, что у него обозначает «равенство». Вычитание он обозначал знаками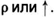

Вот запись уравнения из «Арифметики» Диофанта, которое мы записываем как:

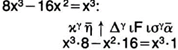
Труды Диофанта долгое время оставались неизвестными для широкого круга математиков и поэтому не оказали заметного влияния на развитие символов — языка алгебры.

В первом алгебраическом трактате аль-Хорезми буквенная символика отсутствовала, поэтому и в трудах европейских математиков символика появилась гораздо позже.

Значительный вклад в развитие языка алгебры — символики внес француз Франсуа Виет (1540—1603). Юрист по образованию, Виет служил при дворе Генриха IV. Математикой занимался в часы отдыха. Ознакомившись с учением Коперника, Виет заинтересовался астрономией и решил написать обширный астрономический трактат, но для этого надо было глубоко знать математику. Занявшись изучением математики, он выполнил ряд алгебраических исследований, разработал символику в алгебре, но трактата по астрономии так и не написал.

Во время войны Франции с Испанией Виет оказал большую услугу своей родине — он расшифровал весьма важное письмо испанского двора. Правители Испании, письмо которых было перехвачено, даже не допускали мысли, что такой сложный шифр может быть раскрыт. Впоследствии они приписали раскрытие их шифра волшебству чародея.

В работе «Введение в аналитическое искусство» Виет изложил усовершенствованную им теорию уравнений с применением изобретенных символов. В названном трактате Виет использовал алгебраические выкладки при рассмотрении вопроса геометрии.

Виет ввел в алгебру общую символику. Числовые коэффициенты он стал обозначать согласными буквами и придумал новый термин - коэффициент, позаимствовав из латинского языка слово coefficiens — «содействующий». Знаки + и - он употреблял в современном значении, неизвестные обозначал гласными буквами латинского алфавита, а вместо А² писал: «А квадратное»; знак равенства записывал словом. Выражение х³ + Зbх = 2 с у Виета выглядело так:

Дальнейшее значительное усовершенствование алгебраической символики принадлежит Рене Декарту. Он ввел для обозначения коэффициентов строчные буквы латинского алфавита: а, b, сит. д., а для обозначения неизвестных — последние буквы того же алфавита — х, у, z... Это нововведение получило широкое распространение в работах математиков и с небольшими изменениями сохранилось до наших дней.

Пользуясь символами Декарта, выражение x³ + px+q = 0 нужно записать так: x³+px + q 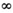0. В этой записи уже и слово равно заменено символом .

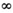После Декарта усовершенствование языка алгебры не закончилось — оно продолжается.