Логарифмы и логарифмическая линейка

По мере развития математики и ее приложений люди стали производить все более сложные вычисления, в частности требующие умножения и деления. Даже у современных ЭВМ и микрокалькулятора на умножение двух чисел уходит в 10 раз больше времени, чем на их сложение. То же относится и к людям, занимающимся вычислениями.

Умножение и деление удалось упростить в XVI в., когда шотландский математик Джон Непер (1550-1617) опубликовал в 1614 г. трактат «Каноническое описание чудесных логарифмов»-так мир узнал логарифмы.

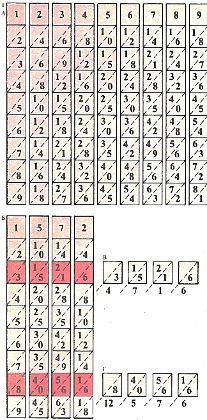
Палочки Непера- это набор из девяти д стержней квадратного сечения (А). Боковая грань каждой палочки разбита на клетки. В первые клетки вписаны номера палочек (от 1 до 9). Остальные клетки разделены диагоналями и перенумерованы сверху вниз числами, образующими арифметические прогрессии. Номер стержня служит первым членом и разностью прогрессии: клетки стержня 1 перенумерованы числами 1, 2, 3, ..., 9; стержня 2-числами 2, 4, 6, ..., 18; стержня 3-числами 3, 6, 9, ..., 27 и т. д. Клетки стержня 9 перенумерованы числами 9, 18, 27, ..., 81. Аналогичным образом разбиты на клетки и перенумерованы остальные грани каждого стержня.

Чтобы найти кратные какого-нибудь числа, например 1572, нужно вынуть стержни 1, 5, 7 и 2 из коробки и уложить их рядом (Б). Если требуется найти 3 * 1572, то следует отсчитать третий сегмент сверху и сложить числа по диагонали (В)- мы получим 4716.

Чтобы найти 8 • 1572, нужно соответственно отсчитать восьмой сегмент сверху (Г): получим 12576.

Если 1572 требуется умножить на число больше 9, например на 38, то находятся произведения 30 • 1572 и 8 • 1572 (к первому произведению следует приписать нуль справа, так как теперь мы умножаем не на 3, а на 30) и полученные результаты складываются: 38 • 1572 = 47160 + 12 576 = 59 736.

Арифметическая и геометрическая прогрессии. На практике Непер реализовал свои идеи в виде четырехугольных палочек с нанесенными на их грани числами. Палочки Непера позволяли сводить умножение к сложению. Как и логарифмы (или логарифмическая линейка), они основаны на использовании двух прогрессий: арифметической и геометрической.

Арифметическая прогрессия-это последовательность чисел, каждое из которых получается прибавлением одной и той же «разности» к предыдущему. Обычный ряд натуральных чисел-1, 2, 3 и т.д.-арифметическая прогрессия с разностью 1. В геометрической прогрессии каждый член получается из предыдущего умножением на одно и то же число-знаменатель прогрессии.

В прогрессии 2, 4, 8 и т.д. знаменатель равен 2.

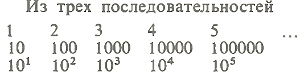
первая-арифметическая, а вторая-геометрическая прогрессия со знаменателем 10. Третья последовательность эквивалентна второй. Она показывает, что показатели степеней числа 10, образующих геометрическую прогрессию, сами образуют арифметическую прогрессию.

Показатели степеней в нижней последовательности называются логарифмами по основанию 10 соответствующих членов средней последовательности. Логарифм-это показатель степени, в которую нужно возвести основание, чтобы получить данное число. Например, логарифм 100 по основанию 10 равен 2 (10² = 100).

Логарифмы, фортепьяно и гитары. Число 10 не единственное основание логарифмов. Первые таблицы были составлены Непером для логарифмов с основанием «е» (иррациональное число). Эти логарифмы (называемые натуральными или неперовыми) и поныне широко применяются в науке. Нажав на клавиши, пианист извлекает звуки, частоты которых относятся как логарифмы с основанием 2, а клавиши располагаются линейно.

Частота любой ноты вдвое меньше, чем у ноты, звучащей выше ее на октаву. Металлические полоски (лады), точнее, расстояния между ними на грифе гитары также образуют логарифмическую шкалу.

Частота любой ноты вдвое выше, чем у ноты, которая на октаву ниже ее. Частоты нот, отличающихся на октаву, относятся как 1:2:4:8:16... Это логарифмическая шкала с основанием 2. Расположение ладов на грифе гитары также соответствует логарифмической последовательности. Прижимая по очереди струны к ладам, гитарист извлекает звуки, образующие хроматическую гамму. Игра на музыкальных инструментах без ладов (например, на скрипке) основана на том же принципе.

При умножении чисел, записанных в виде степеней некоторого основания, показатели складываются: 10² х 10⁴ = 10^{2 + 4} = 10⁶. Поскольку логарифмы-тоже показатели степени, для умножения двух чисел достаточно сложить их логарифмы; тогда по сумме можно найти число, равное произведению. Так умножение сводится к более легкой операции-сложению. Аналогично логарифмы позволяют свести деление к вычитанию.

Для вычислений с десятичными числами таблицы логарифмов необходимо составить только для чисел от 0 до 9,999 (если таблицы четырехзначны; пятизначные таблицы включают числа до 9,9999 и т. д.). Чтобы получить логарифм числа, большего 9,9999, достаточно прибавить к табличному значению целое число (характеристику), равное соответствующему показателю основания-числа 10. Например, четырехзначный десятичный логарифм числа 2 равен 0,3010. Логарифм 200 равен 2,3010, а логарифм 2000 равен 3,3010 (200 = 10² х 10^0,3010 = 10^2,3010, а 2000 = 10³ х 10^0,3010 = 10^3,3010).

Логарифмическая линейка. Логарифмическая линейка - вычислительное устройство, позволяющее умножать и делить числа (с ограниченной точностью). Логарифмические шкалы нанесены на стержни, которые перемещаются друг относительно друга. Отрезки шкал можно складывать и вычитать: в первом случае числа умножаются, во втором делятся. Поскольку шкалы логарифмические, деления к концу линейки сгущаются (как лады на грифе гитары). В отличие от обычной линейки здесь расстояния между делениями образуют скорее геометрическую, чем арифметическую прогрессию.

Простейшая логарифмическая линейка имеет 2 шкалы (на более сложных линейках они обозначены X D). При умножении единицу на верхней шкале устанавливают против одного из сомножителей на нижней шкале и считывают произведение (по нижней шкале) против второго сомножителя на верхней шкале. Чтобы разделить одно число на другое, делимое на нижней шкале совмещают с делителем на верхней и считывают частное с нижней шкалы против единицы на верхней шкале. Прозрачный бегунок с визиром помогает считывать результат.

Точность логарифмической линейки ограничена главным образом ее длиной. В цилиндрических счетных линейках шкалы почти метровой длины навиты на цилиндр, как винтовая резьба. Обычные логарифмические линейки имеют дополнительные шкалы обратных величин, квадратов, квадратных корней и тригонометрических функций.

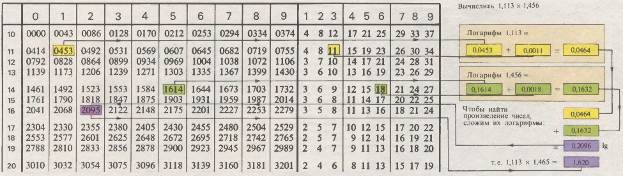
Таблица логарифмов позволяет умножать и делить числа. Логарифм числа 1,113 получен как сумма табличного значения логарифма 1,11 и поправки на 0,003 (сумма равна 0,0464). Логарифм 1,456 вычислен аналогично (он равен 0,1632). Сумма двух логарифмов равна 0,2096. Произведение 1,113 • 1,456 мы находим как число, логарифм которого равен 0,2096. Это логарифм числа 1,620. На практике для получения результата приходится заглядывать также в таблицы антилогарифмов.