Математические кривые. Кривые, уравнения и законы

Всякий, кто способен поймать на лету мяч, имеет интуитивное представление о математических кривых и их преобразованиях в пространстве. Брошенный мяч описывает кривую, близкую к параболе, и многие спортсмены способны предугадать место приземления мяча, когда тот еще только поднимается в воздух. Оценить на глаз, куда попадет мяч, не так-то просто. Мяч на длинной резинке, который используют для тренировки теннисистов, почти невозможно поймать, даже если он пролетает близко и движется медленно: такой мяч описывает кривую, отличную от параболы, и «параболические» рефлексы не срабатывают.

Кривые, уравнения и законы. Системы наведения и управления артиллерийским огнем должны «предсказывать» кривые так же, как это делает спортсмен. Поскольку они не обладают его интуицией, их снабжают быстродействующими ЭВМ, которые вычисляют траекторию снаряда, представляя ее в виде математического уравнения.

Математика - точная наука, и под математической кривой понимают кривую, допускающую точное определение. Оно не обязательно выражается уравнением, в некоторых случаях неформальное описание дает более ясное представление о форме кривой. Например, определение окружности как кривой, все точки которой равно удалены от данного центра, понять легче, чем ее определение как кривой, задаваемой уравнением х² + у² = R².

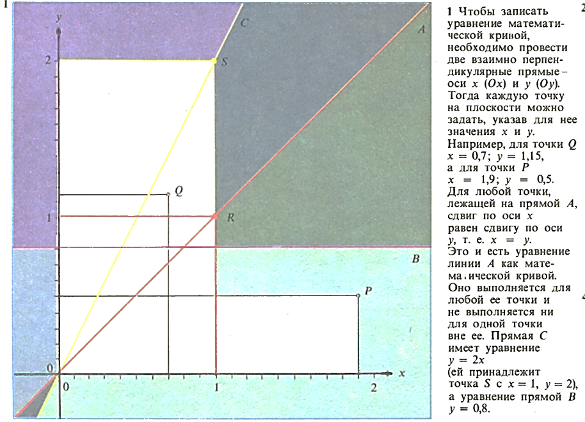
Математика позволяет перевести словесное определение в соответствующее уравнение, выполняющееся для всех точек кривой и не выполняющееся для остальных точек. Свойства кривой легче установить, оперируя символами, а не геометрическими образами. Когда Томас Телфорд (1757-1834) строил в 1826 г. подвесной мост через пролив Менай в Уэльсе, форму цепей он находил, производя измерения на большой модели, сооруженной над сушей,- печальное следствие математической неграмотности. Современный инженер может вывести уравнение троса, поддерживающего мост, и найти из уравнения все, что требуется, не прибегая даже к чертежу.

С математическими законами и математическими кривыми мы встречаемся повсюду. Свободно отпущенный камень падает по прямой, брошенный под углом к горизонту описывает параболу. Луна и искусственные спутники движутся почти по эллипсам, Солнце и Земля имеют почти сферическую форму, поверхность покоящейся жидкости почти плоская все это следствия закона тяготения. Радуга изгибается по дуге окружности, блик на поверхности освещенной солнцем чашки имеет форму острия - это обусловлено законами оптики. Когда люди замечают подобные явления или тригонометрия проводят эксперимент, позволяющий наблюдать их, они открывают научные законы, объясняющие эти явления. Чаще всего ученый обнаруживает математические кривые, только когда вычерчивает их по полученным данным. Уравнение кривой говорит ученому о том, какой «закон» он открыл своим экспериментом.

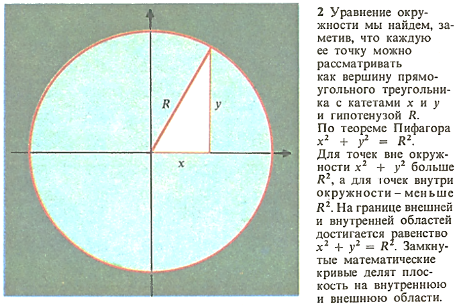
В природе некоторые тела принимают форму сферы под действием приложенных к ним сил, поскольку это форма «наименьшего сопротивления». Капельки воды и мыльные пузыри имеют форму сферы, потому что поверхностное натяжение стремится минимизировать площадь поверхности тела. В старину свинцовую дробь отливали, капая расплавленный свинец с большой высоты в чан с холодной водой. За время падения капли расплавленного свинца застывали в виде шариков и охлаждались настолько, что сохраняли форму при ударе о воду.

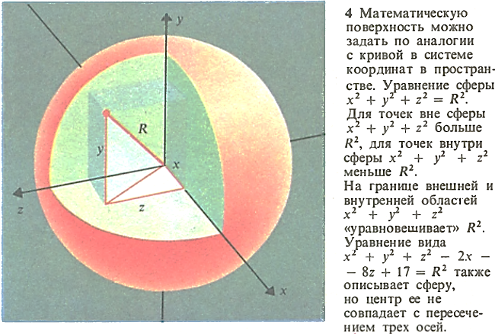
Из теории в практику. Математические кривые и поверхности встречаются во всех областях человеческой деятельности. Например, линзам придают сферическую форму не потому, что это идеальная оптическая форма (хотя она достаточна хороша), а потому, что сферические линзы легче обрабатывать. Сферическая поверхность - единственная из поверхностей, которая сохраняет форму и кривизну независимо от того, как она повернута. Следовательно, трущиеся поверхности, мягкая и твердая, поворачивающиеся то в одну, то в другую сторону, после притирки становятся сферическими, так как только такая форма обеспечивает точную подгонку поверхностей. Таким образом, для получения сферических поверхностей достаточно простого шлифования. Изготовить несферические линзы гораздо труднее, чем сферические.

Цилиндрические тела (трубы, стержни, болты) и отверстия распространены так широко потому, что цилиндрическую поверхность легко изготовить на станках с вращающейся рабочей частью. Бойлеры и котлы высокого давления имеют форму цилиндров, поскольку эта форма обладает большим сопротивлением давлению. Градирни имеют седлообразную форму гиперболоидов, которая хорошо выдерживает свой собственный большой вес и ветровую нагрузку. Духовые инструменты имеют экспоненциально расширяющийся раструб, что наилучшим образом способствует направленному распространению звуковых колебаний.

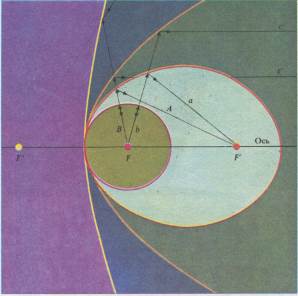
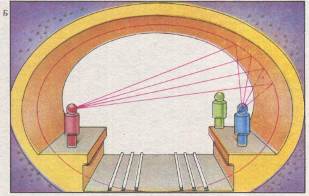
Все конические сечения (А) обладают «зеркальными» свойствами. Эллипс имеет два фокуса: F и F¹; световые лучи, выходящие из одного фокуса, сходятся в другом (А,а). Окружность - эго эллипс, фокусы которого слились в одну точку-центр окружности; световые лучи, выпущенные из него, после отражения вернутся (В,b). Парабола-это эллипс, один из фокусов которого удален в бесконечность. Световые лучи, испущенные из «оставшегося» фокуса, после отражения идут параллельно оси параболы (С,с). Гипербола отражает лучи, исходящие из фокуса F, так, как если бы они шли из фокуса F". Туннели парижского метро имеют в сечении почти эллиптическую форму (Б)

Эстетика и математика. Градирня, трубы духового оркестра, арки мостов и зеркала радиотелескопов имеют формы, хорошо известные в математической физике. Все они, как и другие инженерные сооружения, обладают эстетической привлекательностью, порой недостающей архитектурным сооружениям и автомобилям, облик которых лишен математической завершенности. Та же интуиция, которая помогает человеку воспринимать математические кривые, позволяет ему поймать летящий мяч.

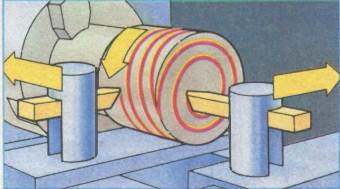
Точка, движущаяся вокруг центра так, что расстояние возрастает пропорционально углу поворота, описывает архимедову спираль. Винтовая линия-это кривая, которую описывает на поверхности цилиндра точка, если пройденное ею расстояние пропорционально углу поворота. Архимедову спираль и винтовую линию можно вырезать автоматически, подводя резец к торцу или боковой поверхности вращающейся детали соответственно.