Множества и группы. Совокупность предметов

Математическая теория множеств была создана Георгом Кантором (1845-1918) и систематизирована Эрнстом Цермело (1871-1953), хотя основные понятия были известны и раньше. Взрослым, которые впервые знакомятся с теорией множеств, ее идеи иногда кажутся трудными, но дети усваивают их легче.

Понятие числа и операции над числами - абстракции, выведенные из опыта, накопленного в сортировке и комбинировании наборов предметов.

Совокупность предметов. Множество-самое фундаментальное понятие математики. Множество-совокупность предметов, обладающих общими свойствами или общим определением. Принадлежность множеству определяется каким-либо правилом или формальным законом. Например, множество океанов определяется так: океаны = {Тихий, Атлантический, Индийский, Северный Ледовитый}, или О = {х|х-любой океан}. Буквой О обозначено все множество, х-переменная, символ I означает «где» или «такой, что». Множества называются конечными, если содержат конечное число элементов (в нашем примере их 4). Множество чисел, называемых при счете, бесконечно, поскольку точно не известно, сколько элементов оно содержит: {1, 2, 3, ...}, или С = {х|х-числа, называемые при счете}.

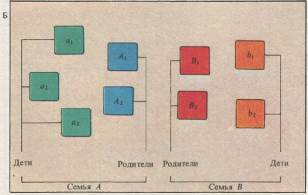
Две семьи (одна с гремя, другая с двумя детьми) образуют универсальное множество (А). Его можно изобразить схематически (Б), обозначив каждый из элементов буквой. Для математических манипуляций над множеством в так называемых диаграммах Венна вполне достаточно букв. Эти диаграммы были введены в 1880 г. английским математиком Джоном Венном (1834-1923).

Множество натуральных чисел J+ = {1, 2, 3, ...} содержит те же элементы, что и множество С. Множества и С называются равными. Множества, содержащие одинаковое число элементов, называются эквивалентными. Например, множество {голубой, зеленый, желтый, оранжевый} эквивалентно множеству океанов: в каждом по 4 элемента.

Понять язык теории множеств удобнее на примере. Универсальное множество (всех рассматриваемых элементов) разбивается на непересекающиеся (не имеющие общих элементов) подмножества. Если существует только два непересекающихся подмножества, то каждое из них является дополнением другого. Примером пустого множества может служить множество слонов, живущих на Северном полюсе: оно не содержит ни одного элемента. Пустое множество принято обозначать ᴓ. Например, на рис. 2 подмножества А и В или Р и С не пересекаются. Их пересечения-пустое множество ᴓ. Понятия разбиения, дополнения, пересечения и объединения являются основными в проблемах классификации и обработки информации.

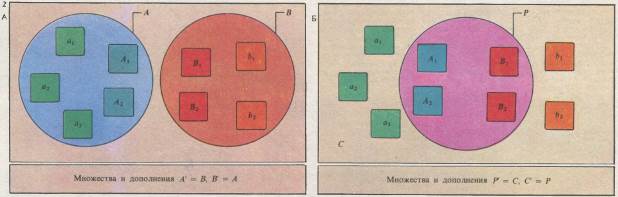
Универсальное множество (рис. 1Б) г можно разбить на два д непересекающихся подмножества. К одному можно отнести членов одной семьи, к другому-другой (А) или к одному отнести родителей, к другому-детей (Б).

В любом случае одно подмножество дополняет другое до универсального множества, поскольку все элементы универсального множества принадлежат одному из двух подмножеств. Отношения дополнительности для 1А: А¹ = В, в' = А.

Дорожная сеть-пример прямого произведения двух множеств, состоящего из всех возможных упорядоченных пар, первый элемент которых выбран из одного, а второй-из другого множества. Прямое произведение иногда называют декартовым в честь Рене Декарта (1596-1650), которому принадлежит идея введения координат. Если X- бесконечное множество точек, образующих прямую на плоскости, а У-бесконечное множество точек, образующих другую прямую, пересекающуюся с первой, то прямое произведение множеств X и У соответствует бесконечному множеству точек, образующему плоскость, которой принадлежат обе прямые.

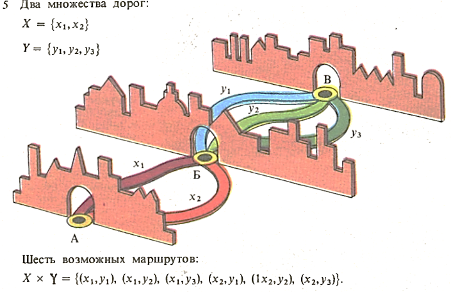
На схеме показаны дороги между городами А и В. Все дороги проходят через Б. Две дороги, ведущие из А в Б, образуют одно множество, а три дороги, ведущие из Б в В,- другое. Существует шесть различных маршрутов из А в В. Они образуют прямое произведение первых двух множеств, состоящее из всех возможных пар, один элемент которых принадлежит первому, а другой- второму множеству. Изучением транспортных сетей занимается топология.

Булева алгебра и алгебра высказываний. Алгебру множеств называют также булевой алгеброй-в честь одного из основателей математической логики Джорджа Буля (1815-1864). Она изоморфна алгебре высказываний в логике. Обе алгебры используют различные обозначения: объединению U и пересечению 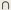в одной соответствуют связки или (V) и и 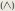в другой. Алгебра высказываний изучает, как истинность составного высказывания зависит от истинности составляющих его высказываний.

Объединение и пересечение в теории множеств соответствуют связкам «или» и «и» в логике. Это позволяет записывать отдельные элементы множеств и их комбинации в виде логических высказываний.

Математическая система возникает, когда к элементам некоторого множества применяется одна или несколько бинарных операций. Одна из наиболее важных систем называется группой. Создателем теории групп был Эварист Галуа (1811-1832), одним из его продолжателей-Артур Кэли (1821-1895). Понятие группы можно пояснить на примере танца, в котором четыре танцора, перестраиваясь, создают различные фигуры. Фигуры танца образуют множество, на котором задана операция-комбинация движений, или перестроение,-обозначаемая 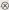. Комбинируя любые фигуры (8Б), мы всегда получим одну из четырех фигур. Единичным элементом здесь является l, и каждый элемент совпадает с обратным. Фигуры удовлетворяют соотношениям (J (g) К) (g) L = L 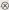L = I и J 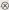{К 0 L) = J (g) J = /, т. е. 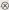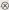сочетательный закон выполняется: (J К) L = J 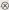(К (g) L). Выполняется также и перестановочный закон: А 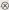В = В (g) А.

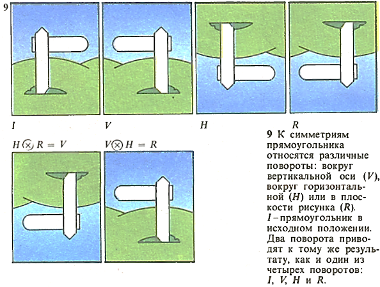
Четыре возможных перемещения прямоугольника образуют множество четырех преобразований. Их можно комбинировать, выполняя одно за другим, т. е. существует взаимно-однозначное соответствие между множеством движений в танце и множеством преобразования прямоугольников. Такие группы называются изоморфными. Поиск изоморфизма-суть математического исследования групп.

О пользе теории групп. Теория групп полезна, например, при изучении числовых систем. Множество всех целых чисел {..., — 3, — 2, — 1, 0, 1, 2, 3, ...} образует группу по сложению (единичный элемент 0). Множество рациональных чисел (если 0 считать рациональным числом) также образует группу по сложению. Если 0 не причислять к рациональным числам, то они образуют группу по умножению. Теория групп не только обогащает теорию чисел, но и приводит к более сложным понятиям колец и полей-множеств с двумя бинарными операциями (сложением и умножением).

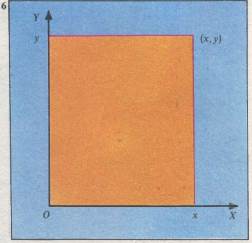
Плоскость, определяемая двумя прямыми, соответствует прямому произведению двух бесконечных множеств (точек на прямых). Точка внутри прямого угла задается координатами х и у и обозначается (х, у). Это прямоугольные координаты. Они широко применяются в аналитической геометрии, где любая линия может быть представлена в виде алгебраического уравнения.