Два способа умножения чисел

Умножение долгое время считалось трудной операцией. Многие математики в XVI в. пытались отыскать более легкий прием умножения, и появилось несколько вариантов умножения. Тогда же был открыт и современный метод под названием «шахматный способ умножения».

В старину многие при умножении пользовались способом умножения решеткой. Для этого один из множителей записывали горизонтально с увеличенными промежутками между цифрами. Под ним вычерчивали решетку в виде клеток, причем каждую клетку делили наклонной линией на два треугольника. Второй множитель располагали справа от решетки и записывали число вертикально сверху вниз, располагая цифры строго против клеток решетки.

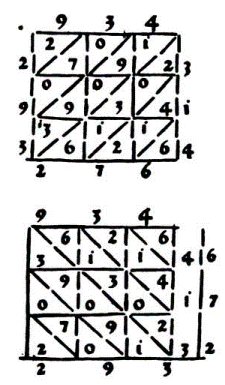
Умножим способом решетки 572 на 361. Умножать начнем с наивысших разрядов. Когда от умножения пары цифр получим однозначное число, запишем его в нижней части клетки, а в верхней части напишем нуль. Если же получим двузначное число, то десятки его запишем в верхней части клетки, а единицы — в нижней. Когда все пары множителей будут умножены и результаты записаны в решетке, произведем сложение цифр отдельно для каждой наклонной полосы. Сложение выполним справа налево. Если при сложении получится сумма двузначная, то запишем только единицы, а десятки прибавим к сумме чисел слева от наклонной полосы. Произведение окажется записанным слева от решетки и внизу нее. Прочитаем ответ: 206 492.

В Италии этот способ умножения называли джелозия, что означает «оконные жалюзи» — решетка.

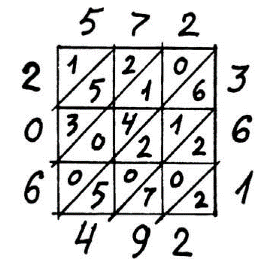
А вот еще один способ умножения, не утративший своего значения и в наши дни. В «Арифметике» Л. Ф. Магницкого, в главе, посвященной умножению, читаем: «Нецыи же умножают странным иным некоим образом... якоже зде умножено есть зри сице

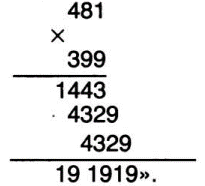
В приведенном способе умножение начато с высших разрядов, а не с низших. В этом и состоит «странность» этого способа.

Академик А. Н. Крылов (1863— 1945) — один из крупнейших математиков и вычислителей — настойчиво советовал начинать умножение с высших разрядов. Особенно следует рекомендовать этот способ при выполнении приближенных вычислений, так как он экономичнее и удобнее обычного — в этом случае при первом же умножении мы получаем важнейшую часть произведения.

Таблица умножения. «Пятью пять — двадцать пять, шестью шесть — тридцать шесть». Все школьники помнят эти две строки из таблицы умножения. Но не каждый учащийся знает, когда и в каком виде она появилась.

Еще в глубокой древности многие математики, чтобы облегчить труд, пользовались таблицами для умножения и деления чисел. Однако вавилонские, египетские, греческие и даже римские таблицы до нас не дошли. Самая ранняя таблица умножения (I в.), дошедшая до нас, по своей форме близка к известной нам так называемой пифагоровой таблице умножения, записанной в квадрате, состоящем из 100 клеток. В ней все произведения чисел от 1 до 10 повторяются дважды.

В книге, изданной в 1496 г., подобная таблица случайно была названа пифагоровой, хотя никакого отношения к Пифагору она не имеет. Все же это название за квадратной таблицей умножения сохранилось и дошло до наших дней.

Недостатком квадратной таблицы умножения является нерациональное повторение произведений: например, в ней записано 4-5 и 5-4. Запоминание таблицы умножения требовало много времени. Поэтому еще в XII в. были созданы треугольные таблицы умножения, в которых одно и то же произведение записано только один раз. Вот какой вид имела усовершенствованная в XV в. таблица умножения.

По этой таблице произведение 7-8 будет соответствовать числу, стоящему в седьмом столбце восьмой строки (цифры над каждым столбцом указывают и номер столбцов).

Математик Аль-Хорезми рекомендовал таблицу умножения заучить наизусть: «И если ты захочешь умножить какое-нибудь число на другое с помощью индийских букв (цифр), необходимо запомнить умножение чисел, которые имеются между единицей и девятью, друг на друга, совпадают ли эти числа или они различны».

В Москве в 1682 г. была напечатана книга «Считание удобное, которым всякий человек купающий и продающий зело удобно изыскати может число всякие вещи». В ней приведены таблицы произведений всех целых чисел от 1 до 100. В пояснении дано описание, как пользоваться данной таблицей. Применяя эту таблицу, без особого труда можно определить, например, произведение 37-26 и др.

В XVIII в. в «Арифметике» Л. Ф. Магницкого таблица умножения дана в рациональном виде. Вот отдельные столбцы из нее:

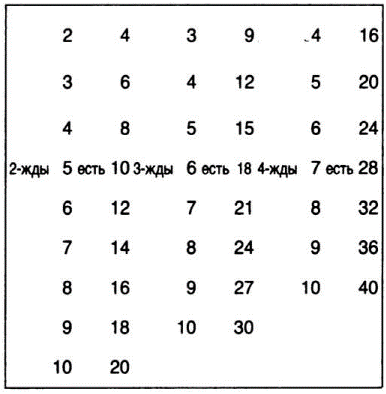
Каждый следующий столбик уменьшается на одну строку, и последний из них имеет вид:

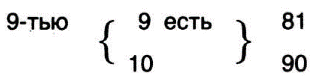
Автор наказывал: «Таблицу надо заучить и всегда ее помнить, а если кто ее забудет, то пользы не будет».