Перспектива углов. Примеры

Впечатление о форме изображаемых на рисунке предметов как плоских, так и многогранных форм во многом зависит от изображения их углов. В перспективном рисунке углы, если их стороны не параллельны картине, изображаются искаженными. Любой угол может быть изображен и острым, и тупым, и прямым. Все зависит от того положения, которое изображаемый угол занимает в пространстве относительно точки зрения и картины. Поэтому умение правильно нарисовать, а если необходимо, то и построить тот или иной угол составляет важную задачу художника.

Перспектива прямого угла. Если одна из сторон прямого угла на горизонтальной плоскости параллельна картине, то другая — перпендикулярна к ней. Поэтому, чтобы построить перспективу прямого угла на горизонтальной плоскости, если одна из его сторон, например AB, параллельна картине (рис. 37), достаточно провести перпендикуляр к ней, т. е. провести другую сторону угла в главную точку картины Р.

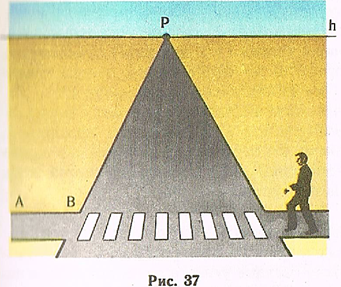
Аналогично можно построить перспективу прямого угла и на вертикальной плоскости, перпендикулярной к картине (рис. 38). Прямая AB параллельна картине. Прямые АР и ВР образуют с ней прямые углы. На плоскости, параллельной картине, изображаемый угол сохраняет свою натуральную величину.

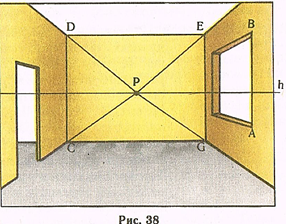
Чтобы построить перспективу горизонтального прямого угла, у которого ни одна из сторон не параллельна картине, нужно построить в плане его натуральное положение относительно картины с вершиной в совмещенной точке зрения Z (рис. 39). Тогда лучи, образующие прямой угол, в пересечении с линией горизонта дадут точки F₁ и F₂, которые и являются точками схода для перспектив прямых, образующих горизонтальный прямой угол. Для построения, например, горизонтального прямого угла на предметной плоскости в точке А и на горизонтальной плоскости, возвышающейся над ней в точке В, достаточно провести лучи из этих точек в точки схода F₁ и F₂.

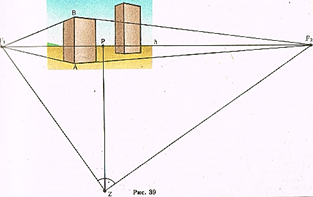
Пример. Построить горизонтальный прямой угол, одна из сторон которого задана горизонтальной прямой AB (рис. 40).

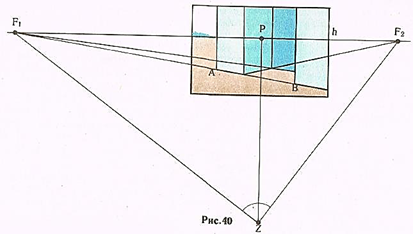
Решение. Горизонтальная прямая AB при продолжении имеет точку схода F₁ на линии горизонта. Натуральное положение прямой AB относительно картины показывает луч, проведенный из совмещенной точки зрения Z В точку F₁. Построим при совмещенной точке зрения натуральную величину прямого угла F₁ZF₂. Точка F₂ и будет точкой схода для всех горизонтальных прямых, образующих с отрезком AB прямые углы. Горизонтальный прямой угол построен.

Биссектриса прямого угла. С помощью биссектрисы прямого угла можно упростить многие перспективные построения. Так, перспективу квадрата можно построить по ее диагонали, которая с является и биссектрисой двух его противоположных углов. Рассмотрим положение биссектрисы прямого угла в перспективном рисунке.

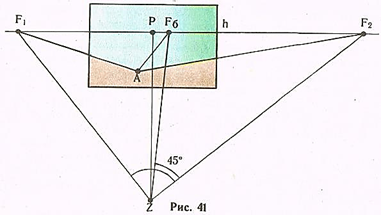
Если в горизонтальном прямом угле F₁ZF₂ при совмещенной точке зрения Z (рис. 41) проведем биссектрису и продолжим ее до линии горизонта, получим точку схода F_б (биссекторную). Прямая AF_б и есть перспектива биссектрисы прямого угла, делящей в натуре угол F₁AF₂ пополам.

Перспектива тупых и острых углов. В рисунке с натуры и при работе над композицией приходится изображать не только прямые, но и острые и тупые углы. Для построения перспективы горизонтального угла нужно построить его натуральную величину с вершиной в совмещенной точке зрения, а затем, продлив стороны до пересечения с линией горизонта, получить точки схода для перспектив его сторон.

Пример. Нарисовать стену с арочным проемом, размещенную к картине под углом 30° (рис. 42). Решение. Выбрав на картине точку А, через которую пройдет направление стены, наймом точку схода для горизонтальных прямых, расположенных к картине под углом 30°. Для этого из совмещенной точки зрения Z проведем луч, параллельный направлению стены, до пересечения с линией горизонта в точке F₁. В этом случае удобнее проводить луч под углом 30° к нейтральной плоскости, так как углы при Z и F₁ равны как внутренние накрест лежащие. Точка F₁ и будет точкой схода направления стены при изображении ее на картине.

Чтобы нарисовать боковые стены арки, составляющие с направлением стены угол 90°, найдем точку схода F₂, куда и проведем прямые верхнего и нижнего оснований арки.