Перспектива параллельных и перпендикулярных прямых. Точки схода

В общем случае перспектива прямой — прямая. В частном случае, когда прямая совпадает со зрительным лучом, она изображается точкой.

В перспективе изображаемые предметы обычно находятся в предметном пространстве. Если провести бесконечную прямую, пересекающую картину и не проходящую через точку зрения, то часть ее, расположенная в предметном пространстве, изображается отрезком.

Пусть даны картина К, точка зрения Z и расположенный в предметном пространстве отрезок В₁С₁ прямой а (рис. 27).

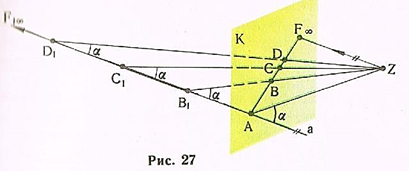
Продолжим отрезок до пересечения с картиной. Точка А — картинный след прямой. Продолжив отрезок в бесконечность предметного пространства, возьмем на нем ряд точек С₁, D₁,..., F_1oo и проведем через них проецирующие лучи. В пересечении с картиной получим точки В, C, D,..., F₀₀. Проецирующие лучи лежат в одной плоскости, которая пересекает плоскость картины по прямой. Поэтому перспектива отрезка есть прямая. По мере удаления точек от картины проецирующие лучи образуют с отрезком все более острые углы а и, когда проецирующий луч направлен в бесконечно удаленную точку F_1oo, он становится параллельным прямой а. В пересечении луча с картиной тогда получим точку F₀₀, которая и является перспективой бесконечно удаленной точки отрезка, продолженного в бесконечность предметного пространства.

Точка F₀₀ называется точкой схода. Она является проекцией несобственной точки пересечения всех прямых, параллельных данной.

Таким образом, для построения перспективы прямой достаточно найти хотя бы две принадлежащие ей точки. Одной из них может быть след прямой или любая другая точка, а второй — точка схода. След прямой находят в пересечении прямой с картинной плоскостью. Точку схода определяют в пересечении с картиной зрительного луча, проведенного параллельно изображаемой прямой.

Относительно картины прямые могут быть параллельными, перпендикулярными и наклонными. Рассмотрим правила их изображения в перспективном рисунке с натуры и при работе над композицией.

Перспектива прямых, параллельных картине. Точки схода параллельных картине прямых расположены в бесконечности, так как зрительный луч, проведенный параллельно им, пересекает картинную плоскость в несобственной точке. Поэтому параллельные картине прямые в перспективном рисунке изображаются параллельно самим прямым. Действительно, любая плоская фигура и линейный угол, образованные параллельными картине прямыми, лежат в плоскостях, параллельных картине, и изображаются подобными фигурами (рис. 28).

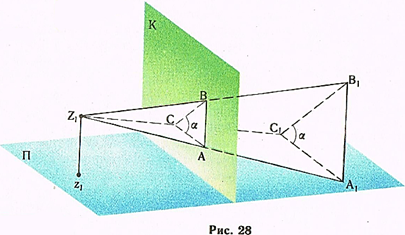
Из этого вытекают такие правила для рисования:
1) прямые, перпендикулярные к предметной плоскости, изображаются перпендикулярными к линии горизонта;
2) горизонтальные прямые, параллельные картине, изображаются параллельными линии горизонта;
3) прямые, параллельные картине, наклоненные к предметной плоскости, изображаются параллельно самим прямым, т.е. их перспектива имеет тот же угол наклона а к линии горизонта, что и они сами к предметной плоскости.

Перспектива прямой, лежащей в плоскости картины, совпадает с самой прямой. Отрезок такой прямой изображается в натуральную величину. Это позволяет использовать отрезки прямых, лежащих в плоскости картины, в качестве масштабов: горизонтальные прямые — как масштаб широт, вертикальные — как масштаб высот.

Перспектива прямых, перпендикулярных к картине. Точка схода перпендикулярных к картине прямых находится в главной точке Р, так как зрительный луч, проведенный параллельно перпендикулярным к картине прямым, пересекает картину в главной точке. Поэтому для изображения перпендикулярной к картине прямой нужно найти перспективу какой-либо второй ее точки. Удобнее такой точкой находить точку пересечения прямой с картиной — картинный след. Поскольку первичная проекция (проекция на предметную плоскость) перпендикулярной к картине прямой также перпендикулярна к картине и имеет точку схода также в главной точке картины Р, то для определения картинного следа, например прямой AB (рис. 29), достаточно ее первичную проекцию продолжить до основания картины в точку с₀, которая и является вторичной проекцией картинного следа С₀. Таким образом, видим (рис. 29), что перспектива перпендикулярных к картине прямых представляет собой связку прямых, сходящихся в главной точке картины Р.

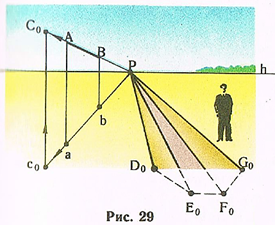
Итак, перспективы прямых, перпендикулярных к картине, и их вторичные проекции имеют одну точку схода - главную точку картины Р.

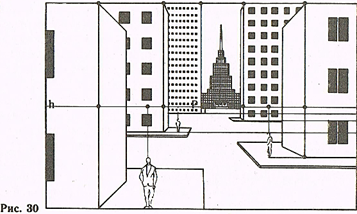
На рис. 30 показано построение перспективы с использованием прямых, параллельных и перпендикулярных к картине.