Уравнения, которыми занимались в арифметике

Многие задачи в математике проще решать применяя уравнения, поэтому уже в I классе ученикам предлагают решать простейшие уравнения, например: х+2 = 8; 14-х=5 и т. п. Но решением сложных задач с применением уравнений занимаются ученики старших классов. Однако есть ряд трудных задач, решить которые легче не применяя уравнений, а посредством использования четырех арифметических действий.

Приведем пример вот такой задачи: «В бригаде было несколько учеников, которые зарабатывали в день по 80 руб. А рабочие этой бригады зарабатывали в день по 150 руб. Вся бригада в составе учеников и рабочих получила за выполнение заказа 1210 руб. Сколько человек было в бригаде?»

Для решения этой задачи примем, что в бригаде х учеников и у рабочих; зарплата (цены условные) учеников составит 80х и рабочих — 150у. Тогда 80х + 150у = 1210 (руб.). Для составления второго уравнения в задаче данных нет. Решение составленного уравнения не дает определенного значения неизвестных, но позволяет выразить значение х в зависимости от у : 80х = 1210 - 150у, или х = (121 -15у) : 8.

Попытаемся решить эту задачу подбором чисел: допустим, что в бригаде был всего один ученик. Тогда на долю рабочих из зарплаты придется 1210 – 80 = 1130. Но это число 1130 не делится без остатка на 150, а число рабочих должно выражаться целым числом. Следовательно, учеников должно быть больше. Если их было 2 человека, то их зарплата составит 80 - 2 = 160 (руб.), а зарплата рабочих будет 1210 - 160 = 1050 (руб.). При делении этого числа на 150 получим: 1050 : 150 = 7, что вполне возможно. Но, может быть, учеников было не 2, а 3 или 4. Проверим эти предположения. Три ученика получат 80 - 3 = 140 (руб.). Тогда рабочие получат 1210 - 240= = 970 (руб.). Однако 970 разделить на 150 без остатка нельзя. Также не делится без остатка на 150 и число (1210 – 80 - 4). Следовательно, условию задачи удовлетворяет только одно решение: учеников было 2, а рабочих — 7. Проверка решения подтверждает правильность этих чисел. Следовательно,

ответом к этой задаче будет 2 + 7 = 9 (человек).

Мы смогли решить приведенную задачу, воспользовавшись дополнительным скрытым указанием, что число рабочих может быть только целым.

Вот еще одна задача, подобная приведенной.

«Вася и Петя коллекционировали монеты. У Пети были только пятачки, а у Васи трехкопеечные монеты. Вася намеревался обменять 6 копеек на пятачки. Сколько пятачков должен был дать Петя, чтобы рассчитаться с Васей копейка за копейку? Сколько монет должен был отдать Вася?»

Составим по условию задачи уравнение: Вася должен отдать Зх (коп.), а Петя даст ему 5у (коп.). Поэтому по условию Зх = 5у. Найти определенное решение для этого уравнения нельзя. Из составленного уравнения выразим х : 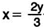. По условию х — целое число не меньше 2. Следовательно, 5у > 3*2. Кроме того, 5у делится на 3. Посмотрим, каким может быть у. Если он равен 1, то (5*1) 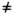6. Возьмем у=2, тогда (5*2) 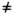6. Возьмем у=3, тогда (5*3) 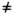6,но —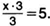

Следовательно, если Вася отдаст 5 трехкопеечных монет, или 15 копеек, то получит от Пети 3 пятачка. Можно получить и другой ответ, но тогда Вася отдаст не 15 копеек, а в 2, 3, 4 и т. д. раз больше. Наилучшим будет решение: Вася отдаст 3*5 = 15 коп., Петя — 5*3 = 15 коп.

Подробное исследование решения задач, похожих на приведенные и более сложных, проводил математик Диофант. Предполагают, что раньше него Архимед тоже знал, как решать такие задачи.

В XII в. приемы решения подобных и более сложных задач изучали ученые Индии. Одним из них был Бхаскара Аскарья.