Как изобразить число отрезком?

Еще Евклид в «Началах» стал изображать значения величин не числами, а отрезками. Каждое число и всю систему рациональных чисел наглядно можно представить на прямой линии. Для этого проведем прямую. Отметим на ней точку и поставим против нее нуль. Эта нулевая точка будет служить началом отсчета. Примем длину какого-либо отрезка за единицу.

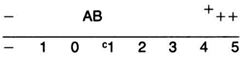
Отложим взятый за единицу отрезок (единичный отрезок) на прямой от нуля вправо так, чтобы один его конец совпал с нулем, а второй расположился бы на прямой правее нуля. Против второго конца отрезка поставим 1. Отложим на прямой отрезок второй раз так, чтобы первый его конец совпал с меткой 1, а второй лег правее. Против этой точки поставим 2. Затем единичный отрезок отложим третий раз, четвертый и т. д. Прямая продолжается бесконечно, и поэтому для каждого числа на ней найдется соответствующее место. Такую прямую называют числовой осью.

Если мы захотим отложить на числовой оси дробное число, то должны разделить отрезок от 0 до 1 на несколько равных частей, например на десять. Тогда дробь 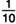будет отмечена точкой А.

Дробь 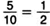изобразится точкой В, а дробь 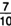точкой С.

Единичный отрезок от 0 до 1 можно разделить на какие угодно мелкие части: на 2,7,10,100,5000 и пр. Следовательно, на этом отрезке можно отложить любую дробь. Так как число делений может быть сколь угодно большим, то, значит, и точек, соответствующих дробям на этом отрезке, может быть любое число. Следовательно, множество дробей, так же как и натуральных чисел, бесконечно. На числовой оси отрицательное число откладывают в левую сторону от нуля. Такое истолкование отрицательных чисел как отрезков, отложенных в левую от нуля сторону, впервые дал в XVII в. Рене Декарт.

В то время ученые трактаты (статьи) писали на латинском языке, поэтому и способ изображения чисел посредством отрезков был назван латинским словом ordinatus (упорядоченный). С приставкой cum (ко), означающей «совместно», это словосочетание означает: совместно заданные числа, определяющие положение точки на плоскости (координаты). Расстояние от нуля по горизонтальной оси названо абсциссой от латинского слова abscissus (отрезанный), а расстояние от горизонтальной оси назвали ордината, т. е. «расставленный в определенном порядке, упорядоченный».

Упражнения и задачи. 1. «Из множества чистых цветков лотоса были принесены в жертву: Шиве — третья долю этого множества, Вишну — пятая и Солнцу — шестая; четвертую долю получил Бхавани, а остальные 6 цветков получил уважаемый учитель. Сколько было цветков?» (Задача Бхаскары.).

2. «Некто сказал другу: Дай мне 100 рупий, и я буду вдвое богаче тебя.

Друг ответил: Дай ты мне только десять, и я стану в 6 раз богаче тебя.

Сколько было у каждого?» (Задача Бхаскары.).

3. «Некто пришел в ряд, купил игрушек для малых ребят: за первую игрушку заплатил 1/5 часть всех своих денег, за другую — 3/7 остатка от первой покупки, за третью игрушку заплатил 3/5 остатка от второй покупки; а по приезде в дом нашел остальных в кошельке денег 1 руб. 92 коп. Спрашивается: сколько в кошельке денег было и сколько за которую игрушку денег заплачено?» (Задача Магницкого из «Арифметики».)

4. «Идет человек от града в другой град, а идет на день по 40 верст, а другой человек идет из другого града в против первого человека, а идет по 30 верст на день. Между же городами 350 верст, и ведательно есть, в колико дней сойдутся оба человека и колико который человек ушел до встречи». (Задача Магницкого. Решить составлением уравнения.)