Сущность центрального проецирования

Изображение точки. Пусть дана точка Z — центр проекций, плоскость П — плоскость проекций и точки A₁, В₁, C₁,D₁ и Е₁. Нужно построить изображение этих точек на плоскости П (рис. 1).

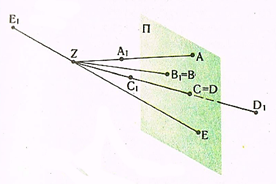
Для этого из точки Z через точку А₁ проведем луч, который будем называть проецирующим лучом (проецирующей прямой), до пересечения с плоскостью П в точке А. Точка А и есть изображение точки А₁, на плоскости П, т. е. ее проекция. Таким же образом найдем и проекции других точек. Так, проекция точки В₁ совпадает с самой точкой (B₁ = В), поскольку точка В₁ лежит в плоскости П. Точки С₁, и D₁ лежат на одном проецирующем луче, и потому их проекции совпадают. Проекция точки Е₁, находящейся дальше от плоскости, чем центр проекций, также будет определяться в пересечении проецирующей при мой Е₁Z с плоскостью П, т. е. в точке Е. Лишь одна точка Z - центр проекций — не имеет определенного решения.

Следовательно, чтобы построить проекцию точки, нужно провести через нее проецирующую прямую и определить точку ее пересечения с плоскостью проекций.

Изображение прямой. Для изображения отрезка А₁Е₁ прямой а₁ на плоскости П (рис. 2) нужно из центра проекций Z через его точки провести проецирующие лучи до пересечения с плоскостью П.

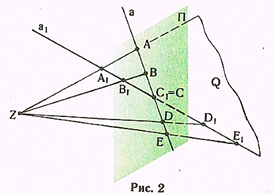
Проекциями точек А₁, В₁, C₁, D₁ и Е₁ соответственно будут точки А, В, С₁ = С, D и Е. Совокупность всех проецирующих лучей, проходящих через точки прямой, образует проецирующую (лучевую) плоскость Q. Она проходит через центр проекций Z. Прямые, принадлежащие одной плоскости и проходящие через общую точку, называются пучком прямых.

Проецирующая плоскость Q пересекает плоскость П по прямой а, являющейся проекцией прямой а₁ на плоскость П. Для изображении прямой достаточно найти проекции хотя бы двух несовпадающих точек. На рис. 2 видим, что прямая а₁ пересекает плоскость П в точке С₁ = С, которая называется следом прямой. След прямой на плоскости П определяется пересечением прямой а₁ с ее проекцией а.

Итак, для построения изображения прямой нужно провести через нее проецирующую плоскость и определить линию ее пересечения с плоскостью проекций. Линия пересечения и есть изображение прямой на плоскости, т. е. ее проекция. След прямой находится в пересечении прямой с ее проекцией.

Несобственные элементы проективного пространства. Основываясь на представлениях евклидова пространства (элементарной геометрии), нельзя решить и объяснить некоторые задачи перспективных построений. Для их решения и объяснения евклидово пространство дополняют несобственными (бесконечно удаленными) элементами: точками, прямыми, плоскостью. Евклидово пространство, дополненное несобственными элементами, называется проективным пространством.

Несобственные точки. Пусть дан отрезок А₁В₁ прямой а₁, пересекающий плоскость проекций П в точке М, и проекция AB отрезка А₁В₁ , построенная из центра проекций Z (рис. 3).

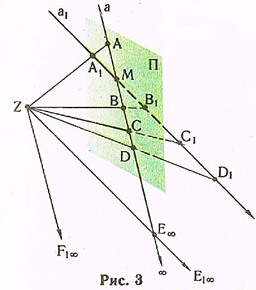
Проведем проецирующую прямую ZE_1oo, параллельную прямой а₁. В пересечении с AB получим точку Е₀₀. Найденная таким образом точка Е₀₀ рассматривается как проекция бесконечно удаленной точки Е_1оо, принадлежащей и прямой а₁. Действительно, если на продолжении прямой а₁ рассмотреть несколько точек, например С₁ и D₁, удаляющихся от точки М, можно заметить, что их проекции С и D приближаются к точке Е₀₀ и совпадут с ней, если их удалять в бесконечность. Таким образом, в пространстве каждая прямая, кроме собственных точек (А₁) М₁, В₁, С₁, D₁), имеет одну особую, бесконечно удаленную, или несобственную, точку Е_1оо, проекция Е₀₀ которой обладает теми же свойствами, что и собственные.

Чтобы найти проекцию несобственной точки прямой на заданную плоскость, нужно из центра проекций провести прямую, параллельную заданной прямой, до пересечения с ее проекцией.

Очевидно, что и прямая ZF_1oo, параллельная плоскости проекций, будет иметь проекцию F₀₀ несобственной точки F_1oo, в которой она пересекается с плоскостью проекций. Но проекция несобственной точки уйдет в бесконечность и не может быть показана на рисунке.

Несобственные линии. Пусть даны две параллельные плоскости Q₁, Q₂ и лежащие в них параллельные прямые a₁ и а₂ (рис. 4).

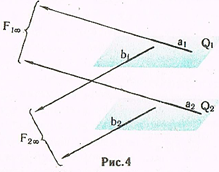
Поскольку две параллельные прямые а₁ и а₂ пересекаются в несобственной точке F_1oo, то точка F_1oo принадлежит и обеим плоскостям. Подобных пар параллельных прямых можно провести множество. И каждая из них будет иметь несобственную точку, например F_2oo для прямых b₁ и b₂. Совокупность этих несобственных точек и представляет собой несобственную прямую пересечения двух параллельных плоскостей. Очевидно, что эта несобственная прямая едина для всех плоскостей, проведенных параллельно заданным.

Две параллельные плоскости пересекаются по несобственной прямой. Чтобы найти проекцию несобственной прямой пересечения параллельных друг другу плоскостей, достаточно найти проекции хотя бы двух принадлежащих ей несобственных точек.

Несобственная плоскость. Дополнение каждой прямой несобственной точкой, а каждой плоскости — несобственной прямой дает множество несобственных элементов пространства, которые в совокупности представляют собой несобственную плоскость.

Из тех знаний перспективы, которые были получены в средней школе, нетрудно заметить, что главная точка картины, точки схода и линии схода — по своей природе не что иное, как проекции несобственных элементов пространства. Поэтому ознакомление с ними поможет глубже понять смысл точек схода и линий схода, которые в перспективном изображении имеют очень важное значение.