История открытие нуля

На первых этапах развития математики люди не ощущали надобности введения нуля. Для счета и действий с небольшими числами он не требовался. Самые древние числа шумеров, которые записывали в шестидесятеричной системе клинообразными знаками, нуля не имели. Например, число 83 они записывали знаками

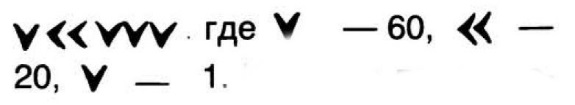
Изменив лишь промежуток между первым клином и десяткой, это число читали как 3623, так как первый клин перед пустым местом означал 60 * 60, т. е. 3600. Такая неопределенность в записи чисел, особенно больших, вносила путаницу в расчеты. Это проявилось прежде всего при астрономических вычислениях, которыми вавилоняне успешно пользовались, удовлетворяя потребностям календаря и мореплавания.

В клинописных записях вавилонян (приблизительно V в. до н. э.) обнаружены на месте пустот знаки такого вида

Такие знаки стали писать, чтобы указать, что в этом числе пропущен один разряд. Учитывая значение указанного символа, число

нужно читать как 60*60 + 10 +10 + 1+1+1, т. е. три тысячи шестьсот двадцать три. Указанный знак у вавилонян выполнял роль нуля, но они не додумались ставить его при необходимости в конце числа. Потребовалось еще около 10 веков, чтобы окончательно решить, где и когда нужно применять нуль и означает ли он число или только цифру.

В индийской математике первоначально нуль тоже отсутствовал.

Продолжительное время и в Индии пользовались десятичной системой, но она не была позиционной. Видимо, после знакомства с вавилонской системой счисления индийские математики стали применять позиционную десятичную систему счисления и запись чисел посредством девяти значащих цифр. После распространения десятичной позиционной системы математики Индии, называя число, например, 3971, говорили: три, девять, семь, один.

Перестановка слов в названии числа не допускалась, так как тогда это было бы иное число. Такой способ счета дал повод неизвестному нам гениальному математику при записи чисел не отмечать каждый раз словом или знаком разряд числа, но располагать разряды числа в строго определенном порядке: на первом месте— единицы, на втором—десятки и т. д., т. е. поступать так, как это делаем теперь мы. В случае отсутствия какого-либо разряда индийцы ставили точку. Так, число 5 * 1 означало 501. Читая его, произносили: пять, сунья, один. Сунья в переводе означало «пусто». В V—VI вв. вместо точки стали писать кружок, который со временем преобразовался в нуль. Индийцы и его называли сунья.

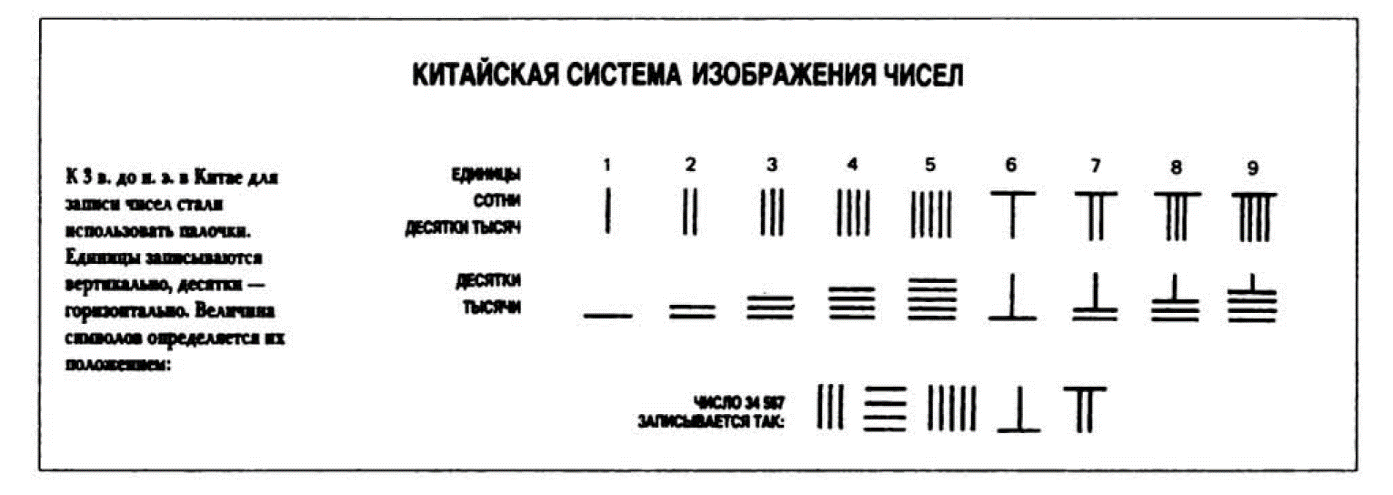
Самую древнюю китайскую математическую книгу относят к X в. до н. э. В то время китайцы пользовались пятеричной системой счисления, но затем ее место заняла десятичная система. Их девять цифр обозначались в виде палочек: I—1, II—2, III—3, IIII —4, IIIII —5, Т —6, TT — 7, TTT — 8, TTTT — 9. Располагать палочки можно было и по-другому. Например, число 6729 можно было записать так:

К применению нуля китайцы пришли значительно позже.

Математики Древней Греции долгое время пользовались буквенной нумерацией и нуля не применяли.

Арабы позаимствовали в Индии цифры, систему счисления и записи чисел. Слово нуль они перевели на свой язык и вместо сунья говорили «сифр». В X—XII вв. индийская система счисления через арабов проникла в Европу, слово сифр не перевели, а немного видоизменили сначала в слово шифр, а позже в слово цифра.

Самый древний документ в Европе, в котором для нуля имеется свой знак (0), относится к IX в. В одной из книг, написанной на латинском языке в XIII в. (тогда все научные работы писали по-латыни), нуль назван «кружок, или цифра, или знак ничего». С тех пор за ним утвердилось название «фигура нуль», что означало «никакой знак». Словом цифра стали называть знаки, обозначающие число единиц в любом разряде, в том числе цифрой назвали и единицу, а позже и сам нуль.

В первом русском учебнике «Арифметика», напечатанном в 1689 г., нуль назван цифрой или ничем. Спустя несколько лет и в России знак 0 стали называть нулем, а знаки чисел 1, 2, 3, 4 ... 9 называли цифрами.

Однако и на этом открытие нуля не закончилось, хотя он приобрел свой вид, получил название, обрел свое место. Но не было решено — нуль цифра или число; если число, то какое: четное или нечетное?

В результате длительных обсуждений математики пришли к заключению: нуль — это число, обозначают его цифрой 0, к натуральному ряду он не принадлежит. С нулем можно производить все действия, за исключением деления на нуль, но сам нуль можно делить на любое число, а также и на два, поэтому нуль отнесли к четным числам. В ряду целых чисел нуль поместился на границе между отрицательными и положительными числами.