Алгоритм и структура математического обеспечения определения кинематических параметров КА

Основной задачей создания математического обеспечения определения динамических характеристик элементов конструкции КА при действии продольного импульса является разработка алгоритма решения дифференциальных уравнений (2.1) с заданными начальным условием и структурой математического обеспечения.

Анализ работ показал, что для типа уравнений (2.1) можно использовать положительно зарекомендовавшие себя методы типа Рунге—Кутта. В качестве программы для решения системы дифференциальных уравнений была выбрана подпрограмма Фелиберга RKF-45.

Подпрограмма требует шести вычислений функции за шаг. Четыре из этих значений берутся с одним набором коэффициентов, что приводит к системе четвертого порядка, и все шесть значений комбинируются с другими коэффициентами, что дает уравнение пятого порядка. Сравнение двух вычисленных величин позволяет получить оценку ошибки, которая используется для контроля длины шага. При работе программы широко используются линейная и параболическая интерполяции.

Линейная интерполяция основана на использовании следующего выражения (при условии, что аргумент находится между точками X_i и x_i+l):

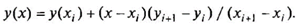
Параболическая интерполяция основана на использовании интерполяционной схемы Лагранжа, примененной для определения парабол второго порядка. При составлении программы применен алгоритм.

Для расчета динамических характеристик конструкции КА, находящегося под действием продольного импульса, разработаны алгоритм и программы. Программа предназначена для определения перемещений, скоростей и ускорений, возникающих на элементах конструкции под действием нагрузки. Информация о топологии исследуемой структуры вводится с помощью матрицы смежности.

В программе предусмотрен ввод характеристик связей как в виде интерполяционного (аппроксимационного) полинома, так и в виде произвольной функциональной зависимости, задаваемой таблицей. Для наиболее часто встречающихся типов нелинейных связей в программу встроены описывающие их функции. Входное воздействие может быть приложено в любой точке исследуемой структуры. Вид воздействия выбирается пользователем программы из набора готовых функций или задан в виде таблицы.

Жесткостные и демпфирующие связи могут быть как линейными, т.е. характеризоваться постоянными коэффициентами жесткости и демпфирования, так и нелинейными, когда жесткостные характеристики представляются в виде полиномов по степеням деформации, а демпфирующие — по степеням скорости деформации:

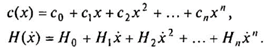
Программа написана на алгоритмическом языке “С”.

При наличии у персонального компьютера стандартной оперативной памяти программа позволяет производить расчеты для систем, имеющих более 100 узлов.

Структурно программа NELDER (“нелинейное дерево”) состоит из семи модулей, иерархия которых показана на рис. 2.3.

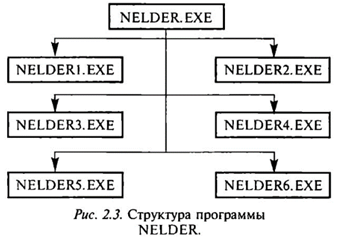
Функциональное назначение модулей:

NELDER — управляющая программа. Выводит на экран главное меню. По указанию пользователя формирует список файлов для хранения информации по каждой задаче. По запросам пользователя вызывает программы NELDER 1-NELDER6.

NELDER 1 — программа, позволяющая в диалоге с пользователем-сформировать структуру механической системы, ввести все исходные данные по ней. По запросу производится вывод на печать;

NELDER 2 — программа расчета собственных частот конструкции. Выдает также рекомендации по шагу расчета, который запрашивает;

NELDER 3 — программа, запрашивающая у пользователя информацию о начальных условиях для расчета ускорений, скоростей и перемещений во времени и по возможности автоматизирующая процесс задания этих величин;

NELDER 4 — программа расчета ускорений, скоростей и перемещений узлов системы во времени;

NELDER 5 — программа, выводящая по запросам пользователя графики рассчитанных функций на экран или на печать;

NELDER 6 — программа, создающая на экране дисплея подвижную картину возмущенного движения конструкции во времени; в пошаговом режиме позволяет выводить на печать любое деформированное состояние системы.

Программный комплекс позволяет:
- в диалоге с пользователем формировать любую структуру механической системы;
- вводить в удобной форме все исходные данные;
- задавать любые начальные условия;
- определять собственные частоты системы и получать рекомендации по шагу расчета;
- производить расчет ускорений, скоростей и перемещений узлов системы во времени, а также деформаций связей;
- выводить любые рассчитанные функции в виде графиков на экран или принтер;
- получать на экране мультипликационную картину возмущенного движения системы во времени.

С целью проверки точности выполнения расчетов по разработанной программе был проведен анализ решения характерной задачи путем сравнения его с точным аналитическим решением.

Для анализа был выбран фрагмент динамической схемы реальной конструкции КК (РБ), представляющей собой две сосредоточенные массы, соединенные между собой упругим стержнем. К сосредоточенным массам прикреплены осцилляторы (рис. 2.4).

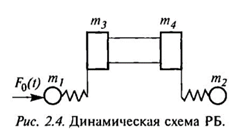
К одному из них приложена внешняя сила, изменяющаяся по треугольному закону с различными градиентами нарастания и спада (рис. 2.5, табл. 2.5).

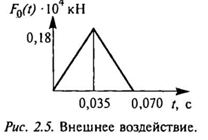
Парциальные частоты осцилляторов m₁ и m₂ равны 14,74 и 35,09 Гц соответственно. Частота первого тона собственных колебаний стержня — 1110 Гц.

Для динамической модели, изображенной на рис. 2.4, существует точное аналитическое решение. Оно получено из решения системы уравнений, описывающих колебания рассматриваемой динамической модели при воздействии внешней силлы:

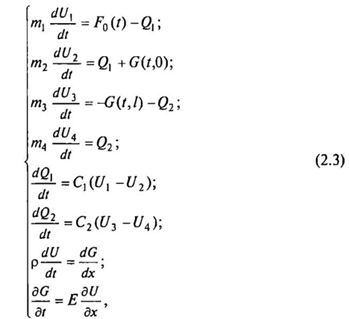
Параметры процесса (скорости колебаний осцилляторов, перегрузка и частота колебаний) определены путем решения системы уравнений (2.3) с помощью преобразований Лапласа.

Последовательность решения изложена в и выполнена следующим образом.

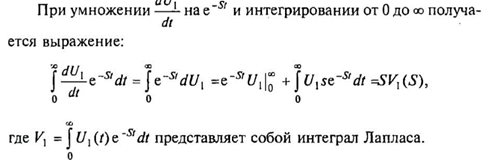
Система уравнений (2.3) в пространстве изображений запишется так:

Общее решение системы ищется в видe

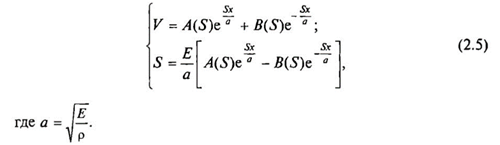
A(S) и B(S) определяются подстановкой (2.5) в (2.4).

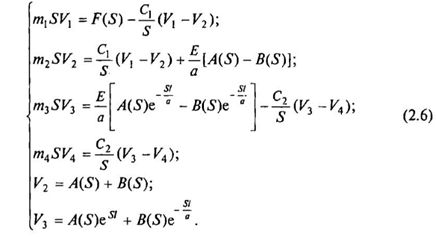
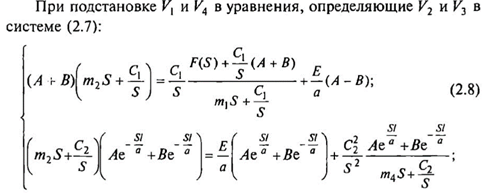
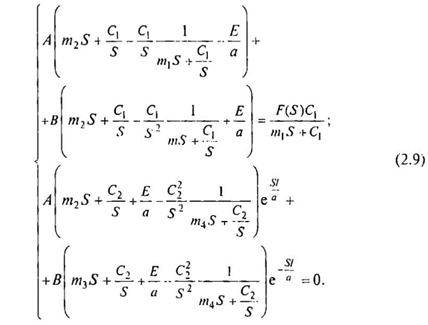
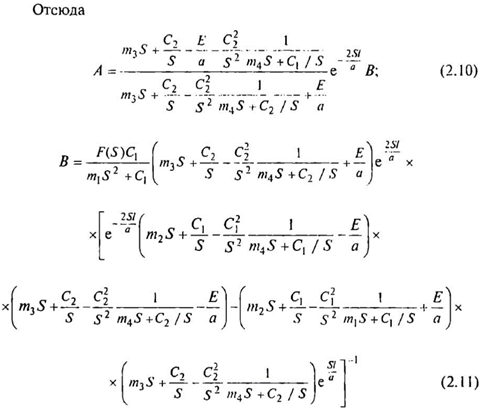
При введении упрощений

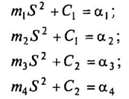
и с учетом того, что

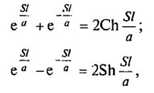
выражения (2.10) и (2.11) принимают вид

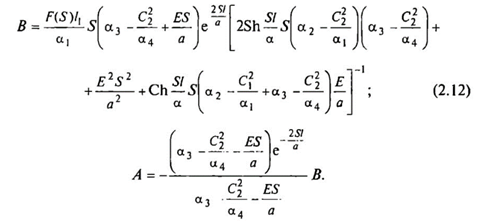
При подстановке выражений для А и В в систему (2.6) вычисляются значения V₁-V₄

Для восстановления скоростей по их представлениям по Лапласу используется формула обратного преобразования Лапласа:

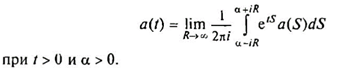
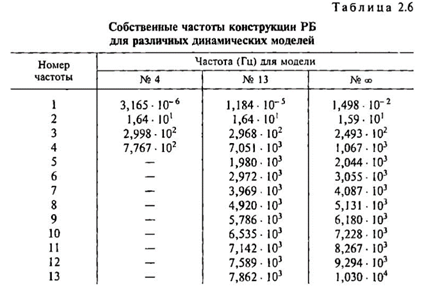
Вычисление интеграла обратного преобразования для рассматриваемого подынтегрального выражения производится по программе. Первые собственные частоты рассматриваемой динамической модели РБ приведены в табл. 2.6.