Математическая модель ЭДВ

ЭДВ представляет собой электромеханический преобразователь энергии, состоящий из электрической и механической систем. Наиболее общим подходом при описании таких систем является уравнение Лагранжа:

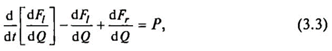
где F₁, — разность кинетической и потенциальной энергии системы; F_r — энергия рассеивания; Р— вектор внешних сил; Q — вектор обобщенных координат системы. Дифференцирование в (3.3) производится по всем компонентам вектора обобщенных координат.

Электрическая система содержит подвижную и неподвижную обмотки, на которые подаются соответствующие напряжения U₁ и U₂- При рассмотрении электромагнитных процессов приняты следующие допущения [72]: проводимость магнитного потока в магнитопроводе бесконечно велика; эффект вытеснения тока в проводниках отсутствует; индукция не зависит от распределения тока в поперечном сечении проводника; электрическая энергия контуров значительно меньше магнитной энергии; пространство, окружающее обмотки, однородно. Обобщенными координатами электрической системы являются токи i и заряды q в обмотках подмагничивания и подвижной.

Механическая система содержит упругую диафрагму с коэффициентами жесткости к и демпфирования h, на которой закреплена подвижная система ЭДВ массой т. На механическую схему извне действует некоторая сила F_вн, которая представляет собой реакцию нагрузки на действие ЭДВ. Обобщенными координатами механической системы являются скорость V и перемещение X подвижной системы. С учетом этого функции F₁ и F₂ примут вид

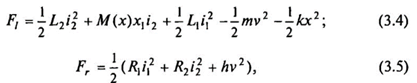
где L₁ и L₂ — индуктивности подвижной обмотки и обмотки подмагничивания; М— взаимная индуктивность обмоток; R₁ и R₂ - сопротивления обмоток.

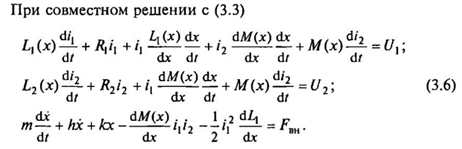
Для создания постоянного потока через зазор ток в обмотке подмагничивания поддерживается постоянным. С учетом слабовыраженной зависимости индуктивности подвижной обмотки от ее перемещения (это в большей степени характерно для ЭДВ, в которых высота подвижной обмотки меньше высоты воздушного зазора) и при введении обозначения

второе уравнение системы становится алгебраическим. Коэффициент BL получил название коэффициента электромеханического преобразования. Тогда, переходя к системе дифференциальных уравнений, описывающих работу ЭДВ, получаем

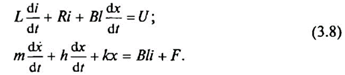
Данная система уравнений от общепринятой отмечается наличием слагаемого F_BH, которое отражает реакцию нагрузки на действие ЭДВ. В такой записи математическая модель ЭДВ в большей степени обладает универсальными свойствами, поскольку позволяет учесть упругости каркаса подвижной обмотки, различный характер нагрузки (сосредоточенная масса, вязкоупругая нагрузка, осциллятор и др.).

Одним из наиболее удобных и хорошо изученных методов анализа дифференциальных уравнений является аппарат передаточных функций. При использовании преобразования Лапласа и замене 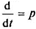структурная схема ЭДВ будет иметь вид, представленный на рис. 3.2.

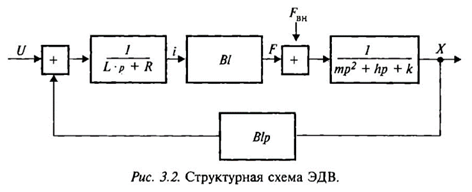
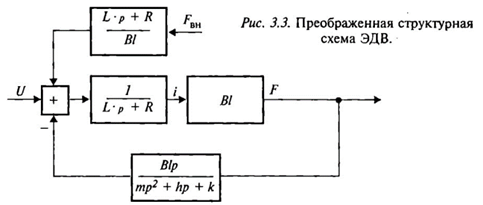
Управляющим воздействием является напряжение U, а выходным — либо перемещение подвижной системы х, либо развиваемое усилие F. При этом структурная схема (см. рис. 3.2) в большей степени подходит для случая, когда выходной координатой является перемещение. В тех же случаях, когда выходной координатой является усилие, эту схему целесообразно для большей наглядности преобразовать (рис. 3.3).

Питание подвижной обмотки осуществляется через усилитель мощности (УМ). Величина выходного сопротивления этого усилителя является критерием деления режимов работы ЭДВ [65, 68, 69J на режим заданного напряжения и режим заданного тока. В первом случае выходное сопротивление усилителя мало 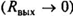, во втором — велико .

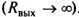При работе в режиме заданного напряжения предполагается, что усилитель мощности является источником ЭДС, характеризующимся параметрами напряжения (U) и внутренним сопротиапени- ем 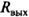, которым либо пренебрегают, либо учитывают соответствующим увеличением активного сопротивления подвижной обмотки. ЭДВ описывается передаточными функциями по задающему (U) и возмущающему 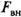воздействиям. Если выходной координатой является перемещение, то передаточные функции будут следующими:

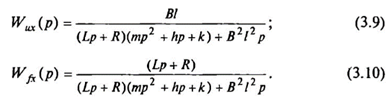
Если выходной координатой является развиваемое усилие, то

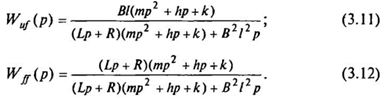
Характеристическое уравнение ЭДВ:

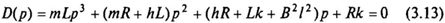
имеет три корня. Если не приняты специальные меры по искусственному изменению характера корней, то в (3.13) один из них действительный и пара — комплексно-сопряженных корней. Значения этих корней определяются следующим образом:

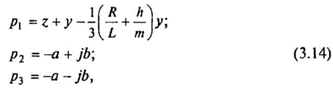
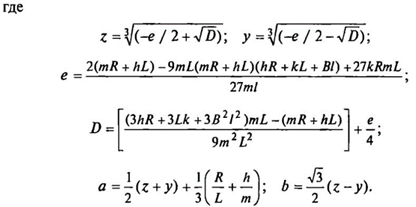
Обычно комплексно-сопряженные корни характеризуют механические свойства ЭДВ (b — частота механического резонанса; а — коэффициент затухания), а действительный корень — электрические свойства вибровозбудителя ( 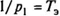— эквивалентная постоянная времени электрической системы).