Математическая модель КА при воздействии продольного импульса

Наиболее приемлемым для рассматриваемых конструкций КА из соотношения точности расчета динамических нагрузок и минимальности затрат на вычислительные процессы является метод сосредоточенных параметров, применяемый в соответствующей динамической модели конструкции. При построении динамических моделей с сосредоточенными параметрами приняты следующие допущения:
- масса аппарата представляется системой дискретных масс, определенным образом соответствующих компоновочной схеме КА;
- массы соединены невесомыми пружинами и демпферами;
- характер демпфирования (при отсутствии специальных диссипативных элементов) соответствует гипотезе вязкого трения;
- массы оболочек и стержневых конструкций распределяются между элементами их закрепления (шпангоутами);
- навесные элементы (антенны, двигатели и т.п.) представляются в виде отдельных прикрепленных к конструкции осцилляторов в количестве, соответствующем числу учитываемых тонов колебаний.

Для определения метода построения дифференциальных уравнений, описывающих динамику, рассмотрена модель с семью сосредоточенными массами (рис. 2.1), первые пять из которых составляют последовательную цепочку. В массе 2 модуля упруго закреплена масса 6, в которой, в свою очередь, упруго закреплена масса 7.

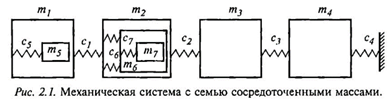
В соответствии с принятым определением динамической модели она описывается системой дифференциальных уравнений, параметры которых определяются свойствами модели.

Для получения дифференциальных уравнений модели в работе использована матрица смежности графа динамической модели. На рис. 2.2 представлен граф механической системы, изображенной на рис. 2.1. Массы динамической модели обозначают вершинами графа 1-7, опора также представлена в виде вершины графа под номером 8. Упругие элементы — ребра графа — обозначены буквами а, в, с, d, e, f, g. Для удобства представления сложных графов используют матрицы смежности.

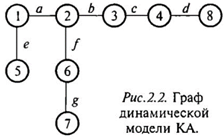
Матрица смежности для графа с n вершинами будет квадратной n*n, состоящей из нулей и единиц. Элемент матрицы a_ij = 1, если существует ребро, соединяющее вершину i с j-й вершиной, и равен нулю в противоположном случае.

При изменении стандартного определения матрицы смежности на место элемента a_ij в случае существования ребра, связывающего вершины і и j, помещается не единица, а обозначение ребра.

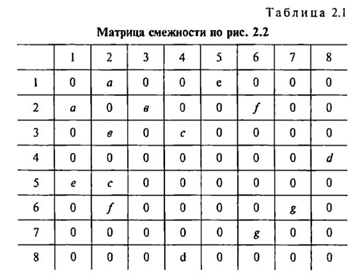
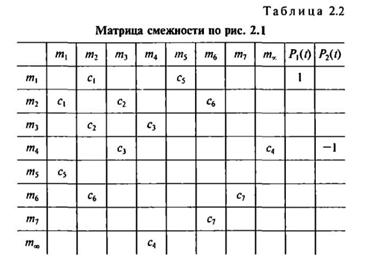
Матрицы смежности графа, изображенного на рис. 2.2 и исходной динамической модели (см. рис. 2.1), представлены в табл. 2.1 и 2.2 соответственно.

Из предположений, что параметры с_i расположены в вершинах некоторых квадратов, а недостающие вершины обозначаются простановкой в них соответствующих жесткостей с обратным знаком, получены результаты в виде табл. 2.3. Пример квадрата показан для жесткости с_6.

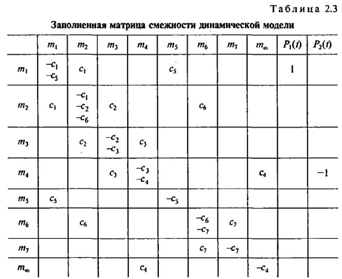
Возможен еще один способ заполнения матрицы коэффициентам — с_i. Для этого в каждой строке матрицы смежности необходимо в элементе т, і поместить с минусом все жесткости, встречающиеся в данной строке.

Следующим шагом является изменение окаймляющих строки и столбца с удалением таковых, соответствующих m_ȹ (табл. 2.4).

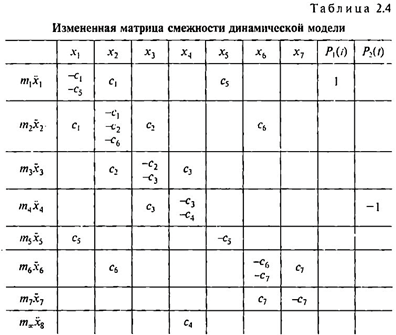
Из табл. 2.4 можно составить уравнения, описывающие динамическую модель, показанную на рис. 2.1, путем умножения каждого элемента i-й строки на соответствующий элемент окаймляющей строки и приравнивая их алгебраическую сумму соответствующему элементу окаймляющего столбца. Получается система уравнений:

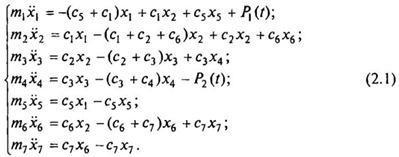
Таким образом, на основе матрицы смежности получены уравнения, описывающие поведение конструкции КА под действием продольной динамической нагрузки.

Учет демпфирования в системе производится таким же способом, только в табл.2.4 необходимо заменить коэффициенты жесткости на соответствующие коэффициенты демпфирования, а перемещения — на соответствующие скорости. Система уравнений (2.1) с учетом демпфирования, представляющая математическую модель исследуемого объекта, запишется в виде:

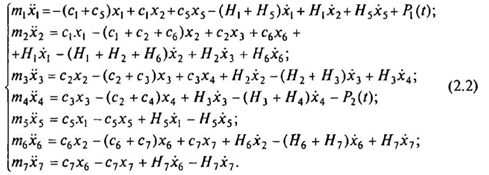
В качестве начальных условий принимаются значения перемещений и скоростей масс, которые присутствуют до приложения к динамической модели рассматриваемого переходного процесса.