Метод сосредоточенных параметров. Метод Бержерона

Метод сосредоточенных параметров. Согласно этому методу реальная конструкция с распределенной массой и жесткостью представляется в виде системы сосредоточенных масс, связанных между собой упругими невесомыми пружинами, имитирующими жесткость элементов системы. Примером такой системы является расчетная схема определения продольных динамических нагрузок элементов космического комплекса.

Уравнения динамического равновесия, описывающие колебания отдельных сосредоточенных масс с учетом диссипативных свойств реальной конструкции, можно получить на основании принципа Даламбера или используя уравнения Лагранжа 2-го ряда. Предполагается, что система совершает малые колебания около положения устойчивого равновесия. Полная кинетическая энергия Т₀ такой системы в общем случае состоит из суммы кинетической энергии ее составных частей:

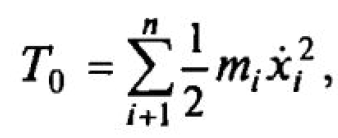
где пі,- — масса і -го элемента динамической модели; х₁- — скорость перемещения і -го элемента динамической модели относительно устойчивого положения.

Потенциальная энергия П₀ системы состоит из энергии деформации, накопленной в ее элементах, и определяется по работе затраченных на деформацию внешних сил:

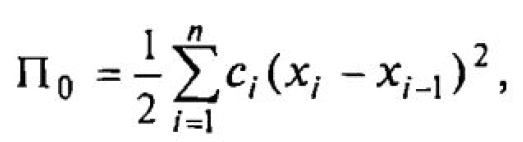
где — C_i коэффициент жесткости i-й упругой связи; X_i — перемещение i-го элемента динамической модели относительно положения устойчивого равновесия.

Диссипативные свойства реальной системы учитываются посредством введения в уравнение движения отдельных элементов функции диссипации Ф, которая записывается в следующем виде:

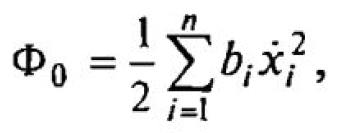
где b_i — коэффициент диссипации.

Диссипативная сила, действующая на i-ю массу, равна:

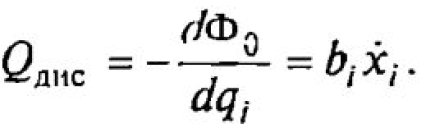
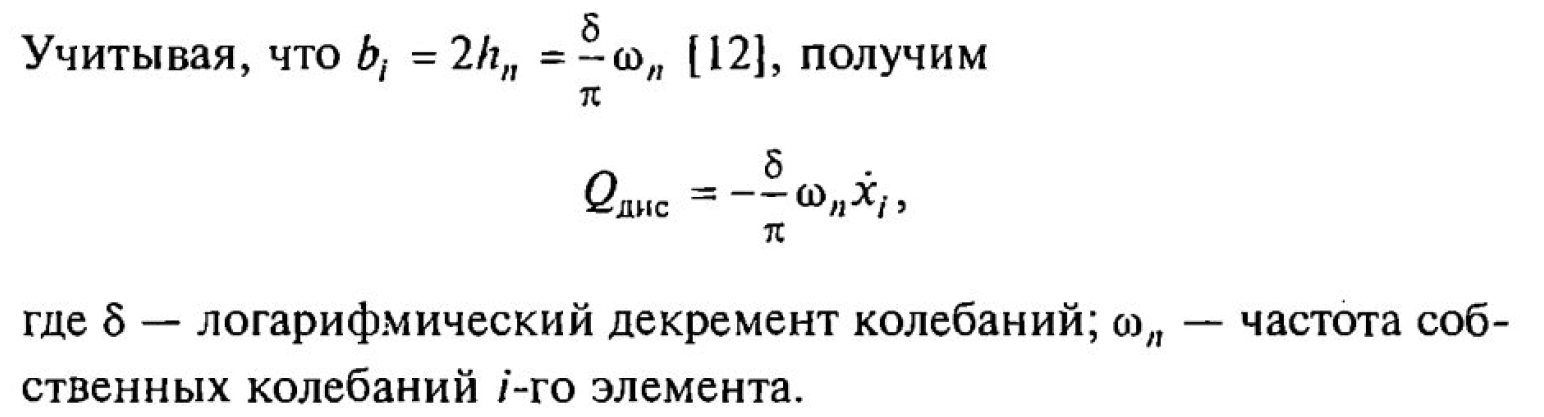
Взяв соответствующие производные от выражений для кинетической и потенциальной энергии, подставив их в уравнение Лангранжа и учитывая при этом диссипацию энергии, можно получить уравнение, описывающее динамическое равновесие отдельной массы динамической модели. Например, для сосредоточенной массы т₂₀ (см. рис. 1.10) уравнение динамического равновесия записывается в виде:

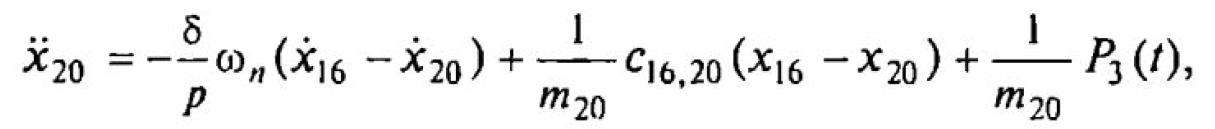
где с_16,20 — коэффициент жесткости упругого элемента, соединяющего массы m₁₆ и m₂₀; Р₃ (t) — внешняя сила, приложенная к массе m₂₀

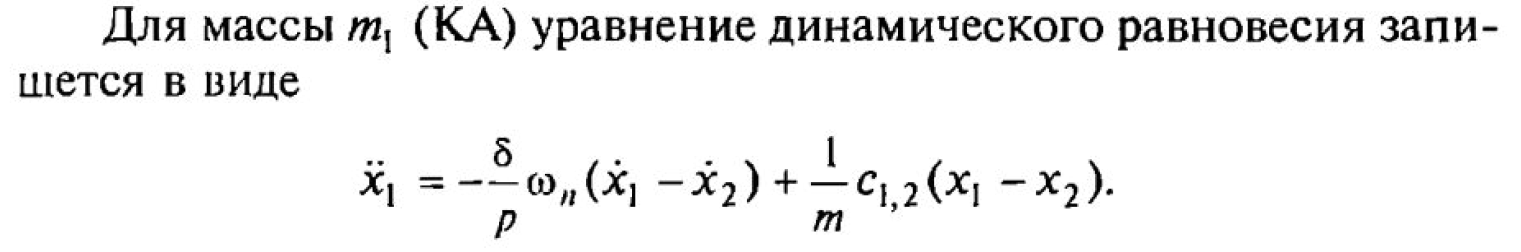
В результате получается система дифференциальных уравнений, число которых равно числу сосредоточенных масс. Полученная система уравнений решается одним из численных методов.

Метод Бержерона. предназначен для расчета динамических моделей с распределенными и сосредоточенными параметрами, включающими в себя участки прямого ступенчатого стержня, соединенные безмассовыми пружинами. В любом сечении стержня могут быть закреплены упруго подвешенные массы и сосредоточенные грузы. В сечениях расчетной динамической модели могут быть приложены внешние силы как известные функции времени.

Каждая из упругих связей модели может иметь нелинейную характеристику, т.е. нелинейную зависимость между деформацией или скоростью деформации упругой связи и усилием в ней. Стержень делится на участки, в пределах которых поперечная площадь сечения и плотность материала остаются постоянными, а на границах участков закреплены либо осцилляторы, либо сосредоточенные массы, либо те и другие вместе. Таким образом, практически любую сложную механическую систему можно свести к набору стыков, каждый из которых описывается системой линейных алгебраических уравнений, определяющих положение его динамического равновесия. Для решения более сложных систем используется метод Гаусса (метод исключения по главным элементам, метод Бубнова— Галеркина). Параметры колебаний динамической модели определяются по совокупности собственных тонов колебаний. В качестве динамической модели принимается аналогичная таковой, рассчитываемой методом Бержерона [52]. Для данной динамической модели строятся системы уравнений движений элементов до и после разделения ступеней PH с использованием свойства ортогональности и введением демпфирования для тонов колебаний.

Для оценки применимости описанных методов проведен расчет динамических характеристик конструкции КА «Радуга» с РБ 11С86 на PH «Протон» (см. рис. 1.10, 1.11). Был выбран один из определяющих максимальное осевое нагружение случаев — отделение первой ступени PH. Демпфирование учитывалось следующим образом:
- для метода сосредоточенных параметров заданием общего для всех упругих связей логарифмического декремента, равного 0,1;
- для метода Бержерона общий декремент колебаний принимался равным 0,1, а для упругой связи КА с PH — 0,2;
- для метода Бубнова—Галеркина задание логарифмического декремента колебаний по тонам таково:

Расчеты проводились по программам, описанным в [52]. Результаты расчетов в виде максимальных значений динамических перегрузок, действующих на КА и элементы РБ, приведены в табл. 1.3.

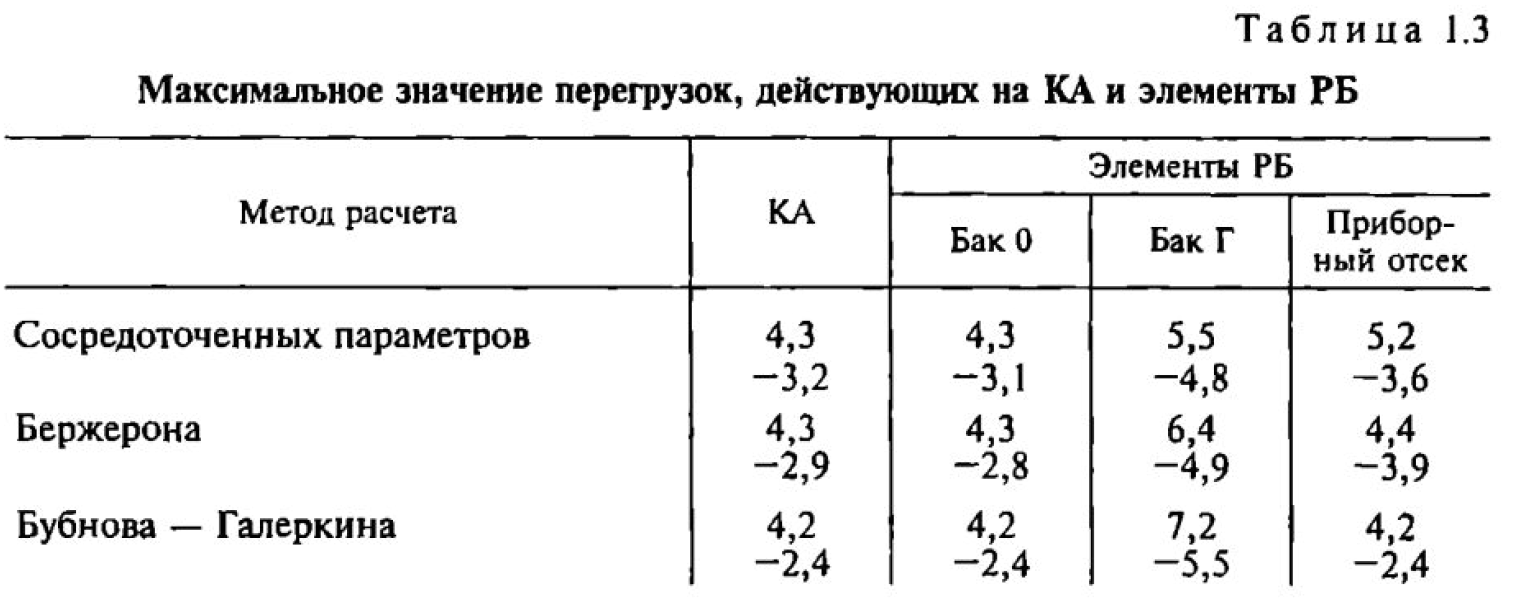
Сравнение максимальных значений продольных перегрузок, действующих на КА и РБ, рассчитанных по трем разным методикам, свидетельствуют об удовлетворительном совпадении, хотя для некоторых элементов в отдельных случаях есть отличия в перегрузках, достигающие 10—25 %. Различия можно объяснить следующим:
- разными способами учета демпфирования;
- разными способами представления в расчетных схемах реальной конструкции.

Анализ результатов расчета динамических характеристик конструкции КА и РБ (см. табл. 1.3) показывает, что для проведения практических расчетов нагрузок на конструкцию КА из соотношения точности расчета и минимальности объема вычислений целесообразно использовать метод сосредоточенных параметров с построением дискретных моделей КА с числом элементов, отражающих основные конструктивные и массовые элементы силовой схемы.