Свободные колебания сложных систем. Спектр

Колебательные системы, описанные выше, например маятник или груз на пружине, характеризуются тем, что они имеют одну массу (груз) и одну жесткость (пружины или нити) и совершают движение (колебания) в одном направлении. Такие системы называются системами с одной степенью свободы.

Реальные колеблющиеся тела (струны, пластины, мембраны и др.), создающие звук в музыкальных инструментах, представляют собой значительно более сложные устройства.

Рассмотрим колебания систем с двумя степенями свободы, состоящих из двух масс на пружинах (рис. 2.1.8). Количество степеней свободы определяется количеством масс (грузов)

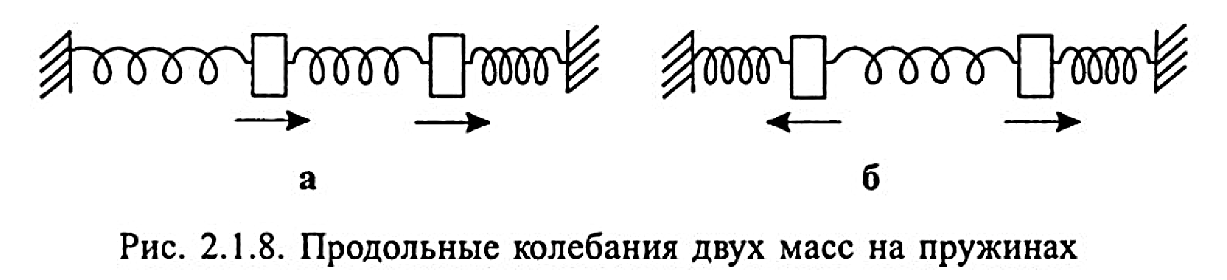
участвующих в процессе колебаний. Такие системы отличаются, во-первых, тем, что они могут совершать колебания с двумя собственными частотами, соответствующими двум формам колебаний (формы колебаний называются модами). Одна форма колебаний соответствует смещению обеих масс в одном направлении, другая форма — смещению в противоположных направлениях (рис. 2.1.8). При этом первая частота колебаний равна:

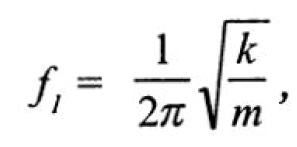а вторая частота, соответствующая второй моде (форме) колебаний, равна: 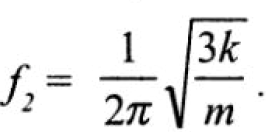Эти две формы колебаний независимы друг от друга (они могут возбуждаться отдельно, могут одновременно как с одинаковыми, так и с разными амплитудами).

Второе отличие систем с двумя степенями свободы заключается в том, что колебания могут происходить в двух направлениях — продольном и поперечном.

Если движения масс происходят в том же направлении, что и сжатие-растяжение пружин, то такие колебания называются продольными (рис. 2.1.8). В том случае, когда массы смещаются в направлении, перпендикулярном пружинам, происходят поперечные колебания. Две формы (моды) поперечных колебаний, которые могут возникать в системах с двумя степенями свободы, показаны на рис. 2.1.9.

Добавление каждой новой массы в такую систему увеличивает число собственных частот и форм колебаний (как продольных, так и поперечных), т. е. увеличивает число степеней свободы.

Если система имеет N масс, то она может колебаться с N продольными и N поперечными модами и иметь соответственно столько же собственных частот продольных и поперечных колебаний. Примеры возможных поперечных колебаний системы даны на рис. 2.1.10.

Все реальные колеблющиеся тела (струны, бруски, мембраны и др.) можно рассматривать как соединение бесконечно большого числа маленьких масс и пружин, т. е. как системы с бесконечно большим числом степеней свободы. Такие системы называются распределенными (в отличие от систем с конечным числом масс и пружин, которые называются сосредоточенными). Например, струна имеет бесконечно много собственных частот и форм (мод) поперечных колебаний, показанных на рис. 2.1.11.

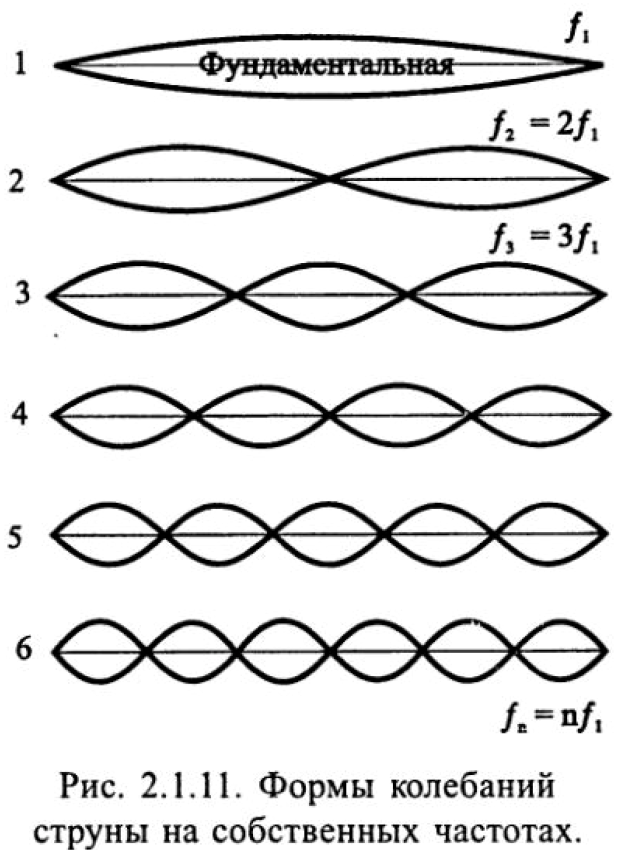
При реальном возбуждении струны в ней обычно возбуждается несколько первых собственных частот, амплитуды колебаний на остальных частотах очень малы и не оказывают существенного влияния на общую форму колебаний.

Вид колебаний (продольных или поперечных) зависит от способа возбуждения. В музыкальных инструментах используются в основном поперечные колебания струн, пластин, мембран, однако в духовых музыкальных инструментах возбуждаются продольные колебания воздушных столбов в трубах. Формы колебаний в открытых и закрытых (с одного конца) трубах показаны на рис. 2.1.12.

При возбуждении реальных тел они совершают колебания сложной формы, которые могут быть представлены в виде суммы одновременных колебаний с различными собственными частотами и амплитудами (метод представления называется анализом Фурье и будет рассмотрен в разделе 2.4).

Набор собственных частот и амплитуд колебаний, которые возбуждаются в данном теле при воздействии на него внешней силы (ударом, щипком, смычком и др.), называется амплитудным спектром. Если представлен набор фаз колебаний на этих частотах, то такой спектр называется фазовым.

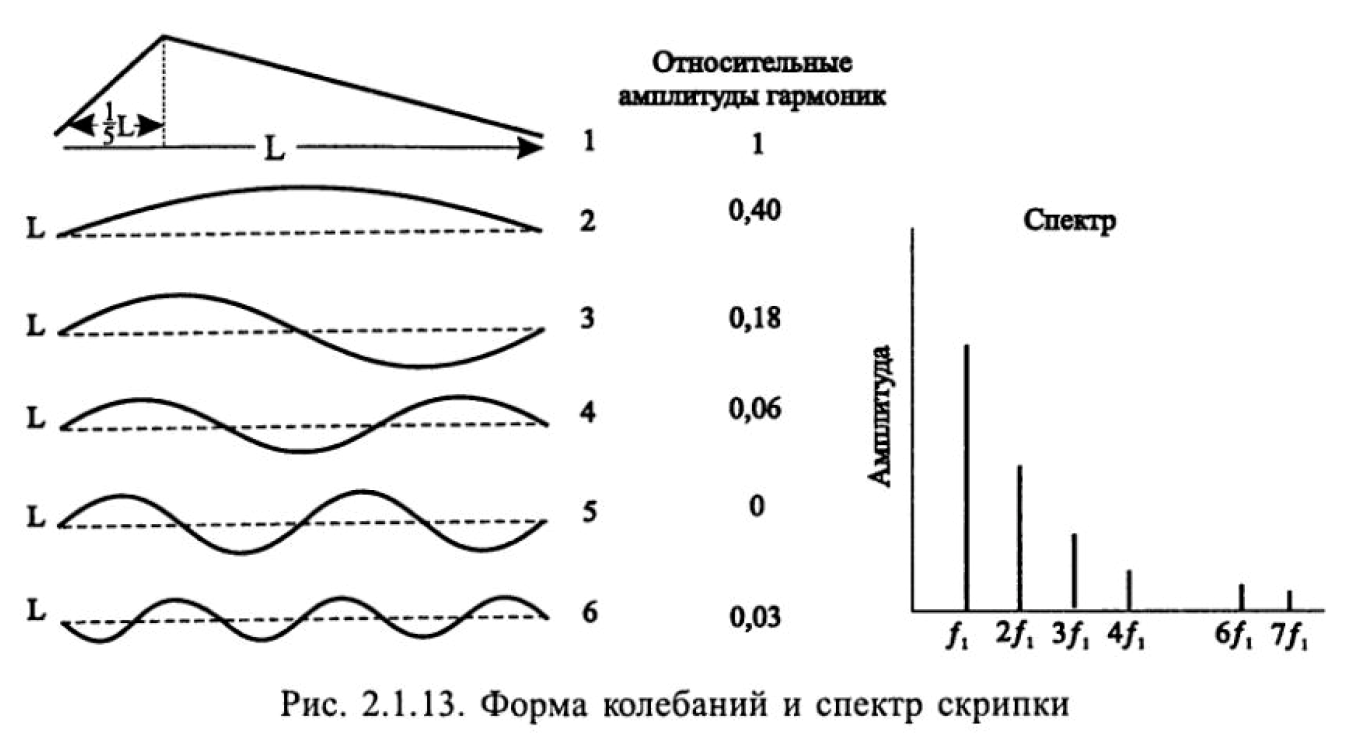
Пример формы колебаний струны скрипки, возбужденных смычком, и ее спектр показаны на рис. 2.1.13.

Основные термины, которые используются для описания спектра колеблющегося тела, следующие: первая основная (низшая) собственная частота называется фундаментальной частотой (иногда ее называют основной частотой). Все собственные частоты выше первой называются обертонами, например на рис. 2.1.14 фундаментальная частота 100 Гц, первый обертон — 110 Гц, второй обертон — 180 Гц и т. д. Обертоны, частоты которых находятся в целочисленных соотношениях с фундаментальной частотой, называются гармониками (при этом фундаментальная частота называется первой гармоникой). Например, на рис. 2.1.14 третий обертон является второй гармоникой, поскольку его частота равна 200 Гц, т. е. относится к фундаментальной частоте как 2:1. (Иногда в литературе используется название всех составляющих спектра — парциалы, включая фундаментальную частоту).

Следует отметить, что не все тела могут быть использованы в качестве вибраторов в настраиваемых музыкальных инструментах, а только те, которые имеют собственные частоты, находящиеся в гармонических отношениях, т. е. у которых все обертоны являются гармониками.