Затухающие свободные колебания

В процессе совершения простых гармонических колебаний происходит переход энергии движения (кинетической энергии), которая пропорциональна квадрату скорости 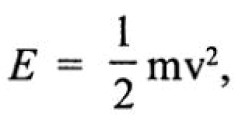в энергию покоя (потенциальную энергию), пропорциональную смещению:

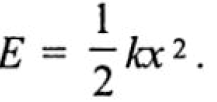
В течение одного цикла колебаний совершается несколько переходов одной формы энергии в другую: в моменты максимального отклонения пружины (маятника, струны и др.) от положения равновесия тело останавливается, в этот момент кинетическая энергия равна нулю, потенциальная энергия максимальна (рис. 2.1.2).

В момент прохождения положения равновесия тело имеет максимальную скорость, и в эти моменты кинетическая энергия максимальна, а потенциальная равна нулю. Если бы эта сумма была постоянна всегда, то любое тело, выведенное из положения равновесия, колебалось бы вечно, получился бы «вечный двигатель». Однако в реальной среде часть энергии расходуется на преодоление трения в воздухе, трения в опорах и т. д. (например, маятник в вязкой среде колебался бы очень короткий отрезок времени), поэтому амплитуда колебаний становится все меньше и постепенно тело (струна, маятник, камертон) останавливается — происходит затухание колебаний.

Затухающее колебание графически можно представить в виде колебаний с постепенно уменьшающейся амплитудой (рис. 2.1.6).

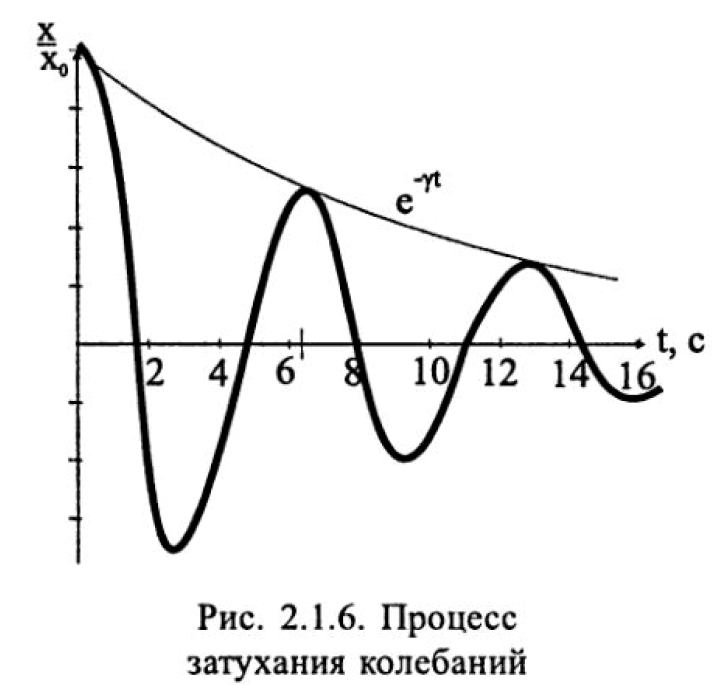
Поскольку процесс затухания определяется в основном силами сопротивления из-за трения в среде (например, в воздухе), в опорах и т. д., эти силы можно считать пропорциональными скорости:

где r — коэффициент внутреннего трения в материале (значения этих коэффициентов для различных материалов обычно даются в справочниках.

С учетом трения второй закон Ньютона может быть записан:

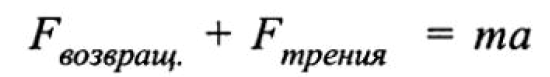
Уравнение (2.1) для случая механических колебаний с учетом затухания будет иметь следующий вид (если 2.4 добавить в уравнение 2.1 и выразить скорость через смещение):

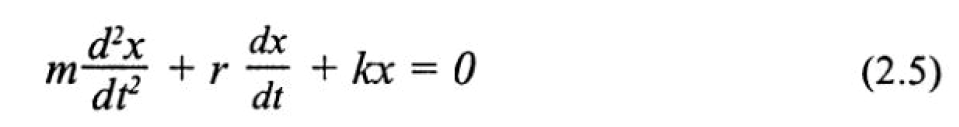
Решение этого уравнения позволяет получить следующую зависимость смещения от времени (рис. 2.1.6 ):

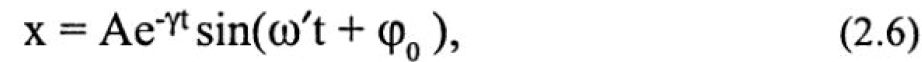
где у — коэффициент затухания; он зависит от массы тела и внутреннего трения материала: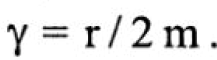

Чем больше коэффициент затухания, тем быстрее затухают колебания (тем быстрее уменьшается их амплитуда). Если масса тела уменьшается, то коэффициент затухания возрастает и колебания быстро затухают, поэтому в рояле верхние, тонкие струны не демпфируются, их колебания и так быстро затухают; на нижних, тяжелых струнах используются демпферы, поскольку их масса большая, следовательно, коэффициент затухания достаточно мал, и они долго колеблются. Коэффициент затухания, а значит, и скорость затухания колебаний зависят также от коэффициента внутреннего трения материала, например в дереве он достаточно большой, поэтому у ксилофона, где используются деревянные пластинки, звук затухает быстро. В то же время в металлических пластинках металлофона звук затухает гораздо медленнее, т. к. коэффициент внутреннего трения в металле меньше, чем в дереве, (звук достаточно долго «звенит»).

Коэффициент затухания у можно определить как величину, обратную времени тс, в течение которого амплитуда колебаний уменьшается в 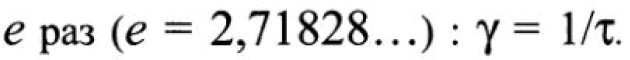Он имеет размерность 1/с. Величина Т с называется постоянной времени.

Для описания процесса затухания механических колебаний иногда используется еще один коэффициент, который называется логарифмический декремент затухания — 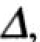, поскольку он достаточно легко измеряется.

Логарифмический декремент затухания определяется как натуральный логарифм отношения амплитуды предыдущей волны к последующей (рис. 2.1.6):

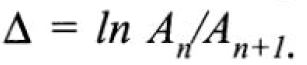
Он связан с коэффициентом затухания следующим соотношением: 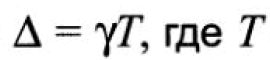— период затухающих колебаний. Чем быстрее затухает колебательный процесс, т. е. быстрее уменьшаются амплитуды, тем больше логарифмический декремент затухания в системе.

В электроакустике, радиотехнике и в музыкальной акустике для определения процессов затухания часто используется величина, называемая добротностью системы — Q.

Добротность Q определяется как величина, обратная коэффициенту затухания:

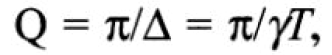
т. е. чем меньше добротность, тем быстрее затухают колебания. Добротность можно представить также в виде 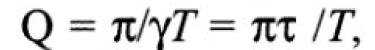т. е. она показывает, сколько периодов укладывается в промежутке времени, равном постоянной времени т (с).

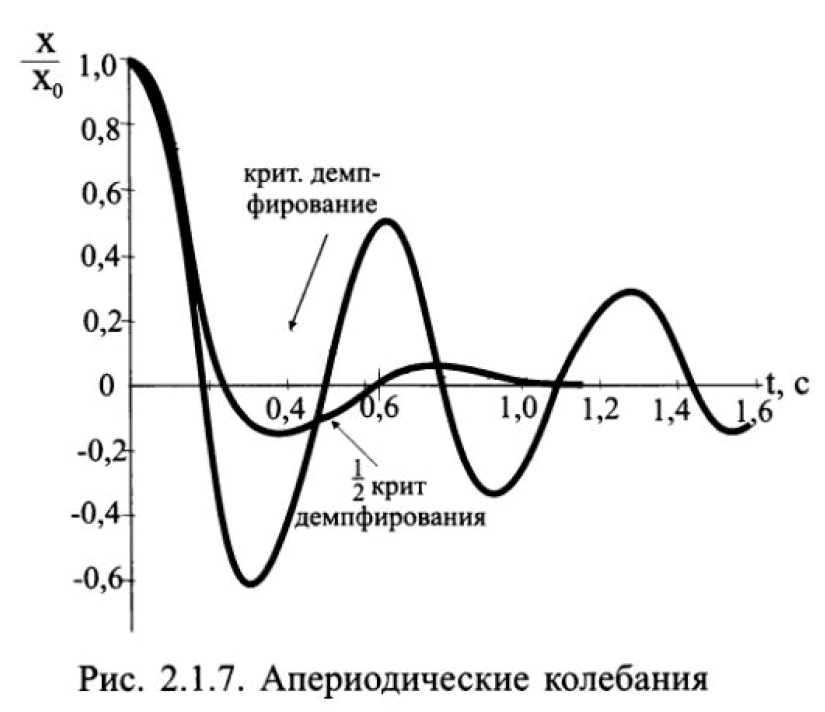
Если Q <0,5, то затухание будет настолько велико, что система вообще не будет совершать колебания, она практически сразу остановится (рис. 2.1.7). Такое движение называется апериодическим. Величина добротности у музыкальных инструментов достаточно большая: камертон Q = 10000, резонатор духового инструмента Q = 10-60 и др. В то же время акустические системы имеют добротность на низких частотах в пределах Q = 0,7-1,2.

При наличии затухания в системе процесс колебания уже не будет, строго говоря, периодическим, т. к. частота колебаний будет уменьшаться с увеличением коэффициента затухания.

В формуле (2.4) значения частоты будут равны: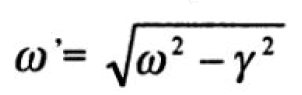

Однако у музыкальных инструментов коэффициент затухания достаточно мал по сравнению с величиной угловой собственной частоты у« од поэтому изменение частоты в процессе затухания будет очень незначительным — можно считать, что в процессе затухания в музыкальных инструментах высота тона практически не меняется.

Необходимо отметить, что процессы затухания звука в музыкальных инструментах имеют огромное значение для идентификации их тембров. Поэтому такое большое внимание уделяется в процессе их изготовления выбору материалов, технологии обработки и т. д., так как от них зависит величина коэффициента затухания и, соответственно, скорость и характер процессов затухания, а значит, и качество звучания данного инструмента.