Простые гармонические колебания (амплитуда, частота, фаза)

Для того чтобы движение было колебательным (т. е. повторяющимся), на тело должна действовать возвращающая сила, направленная в сторону, противоположную смещению (она должна возвращать тело назад). Если величина этой силы пропорциональна смещению и направлена в противоположную сторону, т. е. F = - кс, то под действием такой силы тело совершает повторяющиеся движения, возвращаясь через равные промежутки времени в положение равновесия. Такое движение тела называется простым гармоническим колебанием. Этот тип движения лежит в основе создания сложных музыкальных звуков, поскольку именно струны, мембраны, деки музыкальных инструментов колеблются под действием упругих возвращающих сил.

Примером простых гармонических колебаний могут служить колебания массы (груза) на пружине (рис. 2.1.2).

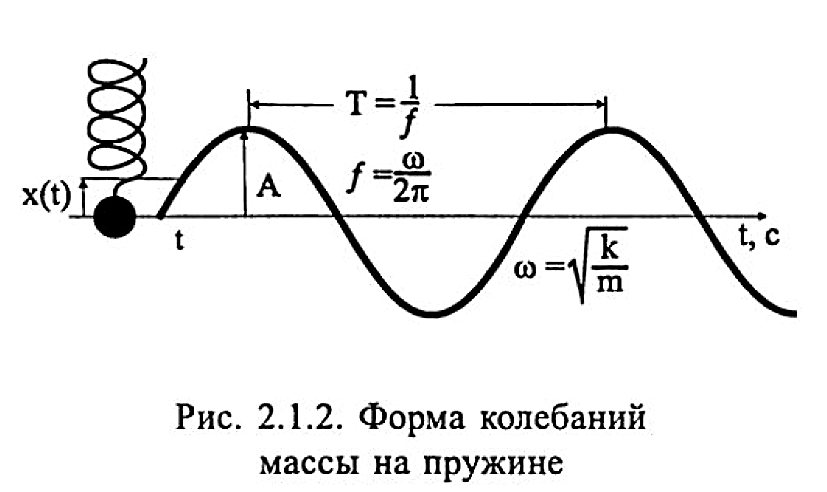
Если массу тела оттянуть из положения равновесия, то на нее начнет действовать возвращающая упругая сила F = - кх (к — коэффициент жесткости пружины), под действием которой она вернется в положение равновесия, «проскочит» его по инерции, сместится в другую сторону, затем под действием той же силы вернется в положение равновесия, после чего цикл движения будет повторяться снова. В этом случае второй закон Ньютона можно записать в виде: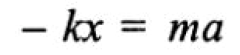

Учитывая, что ускорение а есть производная от скорости или вторая производная от смещения х, получим уравнение:

Эта формула называется уравнением простого гармонического колебания.

Чтобы определить, каким должно быть смещение тела во времени х (t), удовлетворяющее условию (2.1), необходимо рассмотреть форму движения груза на пружине (рис. 2.1.2) или движение маятника (рис. 2.1.3).

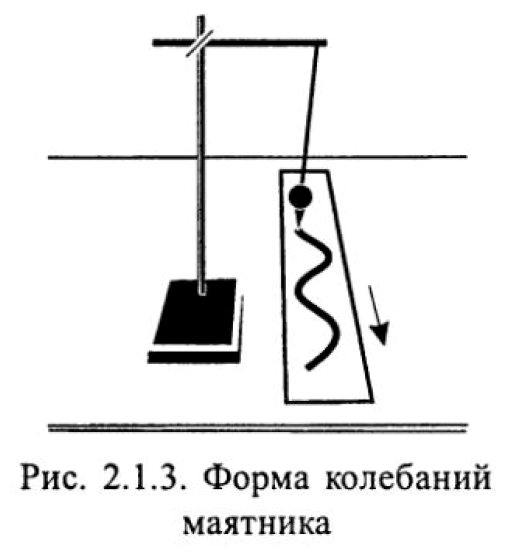
Показанная на рис. 2.3 волнистая кривая, которая описывает смещение тела при гармонических колебаниях, называется синусоидой и записывается в виде:

Таким образом, простое гармоническое колебание можно определить как колебание тела, смещение которого описывается по формуле (2.2).

Колебания тела могут быть периодическими, но несинусоидальными, например смещение струны скрипки (рис. 2.1.4). Здесь движения точки струны повторяются через определенный период, но форма смещения имеет несинусоидальный характер. Однако все сложные периодические колебания могут быть представлены в виде суммы простых гармонических колебаний, подробнее это будет рассмотрено в разделе.

В формуле (2.2) для определения смещения используются следующие величины.

А — амплитуда колебаний. Амплитудой колебаний называется максимальное смещение тела от положения равновесия (при установившихся колебаниях она постоянна) (рис. 2.1.2).

Т — период колебаний. Периодом колебаний называется наименьший промежуток времени, через который колебания повторяются (рис. 2.1.2). Например, если маятник проходит полный цикл колебаний (в одну и другую сторону) за 0,01 с, то его период колебаний равен этой величине: Т = 0,01 с. Для простого гармонического колебания период не зависит от амплитуды колебаний.

Ƒ - частота колебаний. Частота колебаний определяется числом колебаний (циклов) в секунду. Единица ее измерения равна одному колебанию в секунду и называется герц (Гц).

Частота колебаний — это величина, обратная периоду: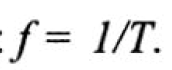

Например, если период колебаний равен Т = 0,01 с, то частота колебаний равна

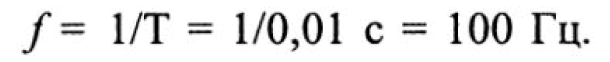
Такая связь между периодом и частотой колебаний характеризует только простое гармоническое колебание.

Частота колебаний связана с высотой музыкального тона: например, нота A4 (ля первой октавы) имеет частоту колебаний 440 Гц. Так же как и период колебаний, частота не зависит от амплитуды колебаний (для малых амплитуд, т. е. линейных колебаний).

ῳ - угловая (круговая) частота. Угловая частота связана с частотой колебаний по формуле

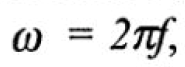, где число 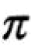= 3,14. Она измеряется в радианах в секунду (pad/с). Например, если частота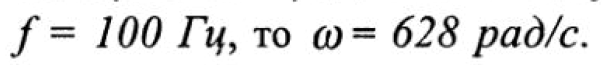

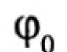- начальная фаза. Начальная фаза определяет положение тела, с которого началось колебание. Она измеряется в градусах. Например, если маятник начал колебаться из положения равновесия, то его начальная фаза равна нулю. Если маятник сначала отклонить в крайнее правое положение и затем толкнуть, он начнет колебания с начальной фазой 90°. Если два маятника (или две струны, мембраны и др.) начнут свои колебания с задержкой во времени, то между ними образуется сдвиг фаз (рис. 2.1.5);

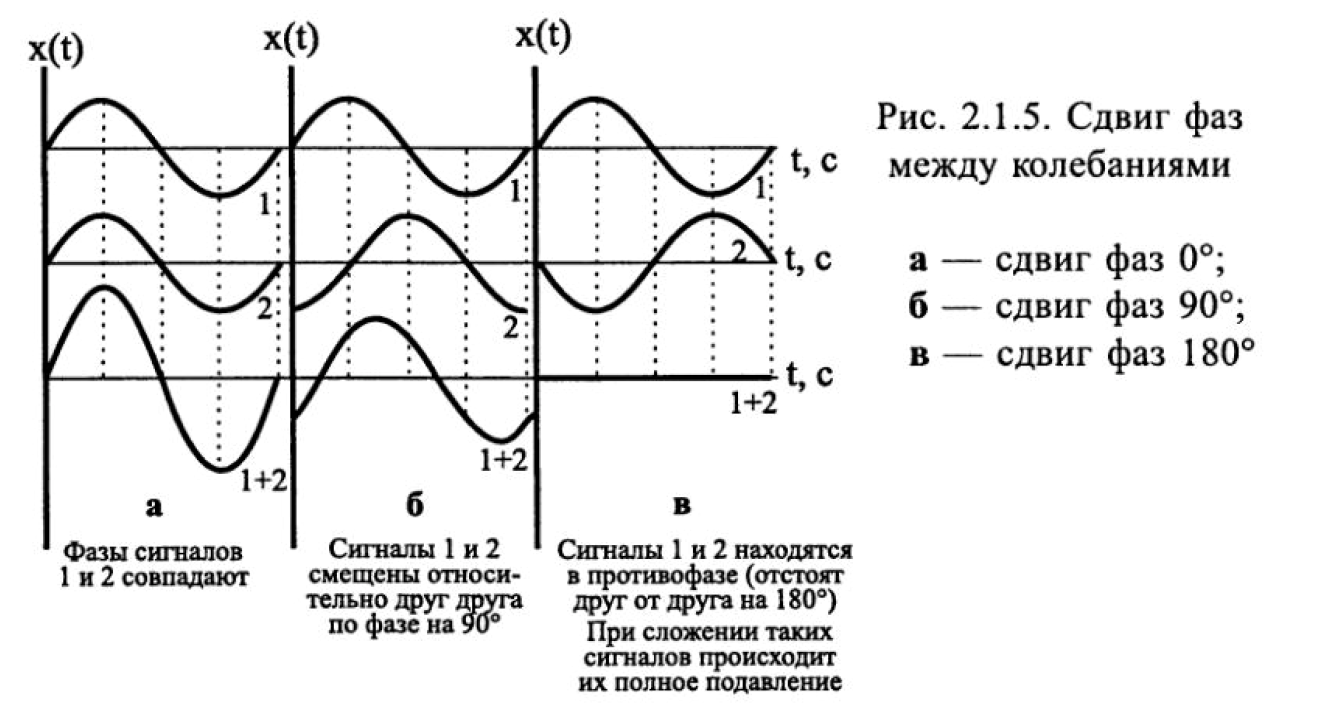
если задержка во времени равна одной четверти периода, то сдвиг фаз — 90°, если половине периода —180°, трем четвертям периода — 270°, одному периоду — 360°.

Если какое-то тело (пружину, маятник, струну, камертон и др.) вывести из положения равновесия (т. е. приложить силу и отпустить), то оно будет совершать свободные периодические колебания с определенной частотой, которая зависит только от его жесткости и массы. Такая частота называется собственной частотой колебаний.

Если подставить выражение (2.2) в уравнение (2.1), то получится следующее выражение (положим начальную фазу равной нулю

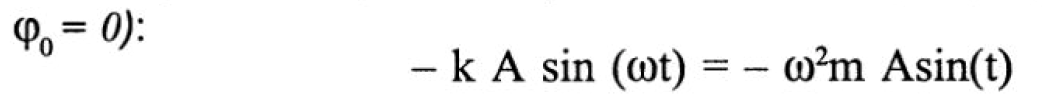
Отсюда, если сократить одинаковые члены, получается, что собственная угловая частота равна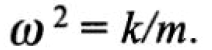

Значит, частота собственных колебаний тела (например, массы на пружине или струны) может быть представлена как:

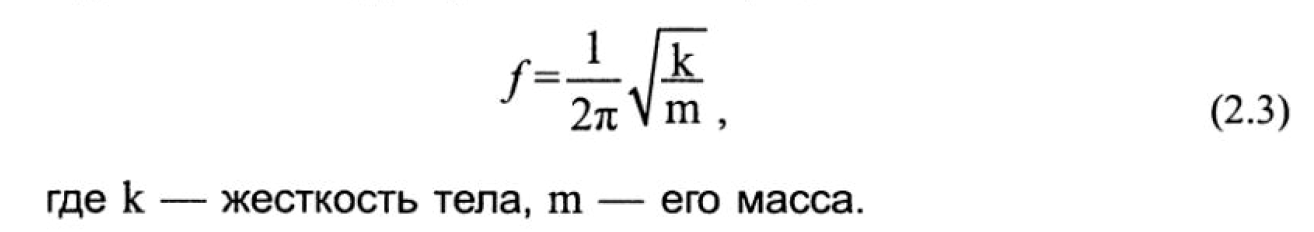
Примеры значений собственной частоты для простых гармонических колебаний можно привести следующие

Маятник длиной L имеет собственную частоту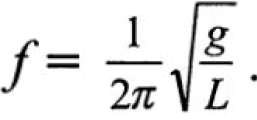

Струна длиной L, массой т и натяжением Т имеет основную собственную частоту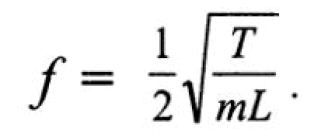

Эту же формулу можно записать в несколько другом виде, если представить массу как произведение поверхностной плотности материала струны на ее длину m = pL , то

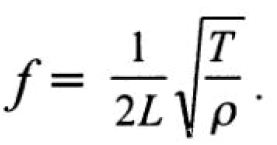
Поскольку, как следует из этих формул, основная собственная частота зависит от силы натяжения, длины и массы струны, то в струнных инструментах (рояль, арфа и др.) низкие ноты извлекают из длинных тяжелых струн, а высокие — из коротких и легких.

Как уже было отмечено, частота собственных колебаний тела не зависит от амплитуды колебаний. Это означает, что можно сохранять высоту музыкального тона (частоту), изменяя его громкость (амплитуду).