Картографическая проекция топографических карт

Земная поверхность не принадлежит к поверхностям, развертывающимся на плоскости, как поверхности цилиндрические и конические, поэтому сферическая поверхность не может быть развернута в плоскость без складок и разрывов, а для изображения земной поверхности приходится прибегать к условным способам построения, называемым картографическими проекциями.

Доказательство Ньютона (1642—1727), что Земля должна иметь вид сфероида или эллипсоида вращения, уже в середине XVIII в. было подтверждено путем так называемых градусных измерений дуг меридианов, позволяющих вычислить длину дуги в один градус, а затем и размеры земного сфероида.

Для всех практических задач геодезии и топографии фигуру Земли достаточно считать сфероидом.

На картах и планах изображают не истинные очертания местных предметов, а проекции их на уровенную поверхность, т. е. на поверхность океанов, мысленно продолженную через материки и острова.

В настоящее время убедились, что в общем Земля, хотя и очень близка к сфероиду, все же представляет фигуру неправильную, не математическую, которую, по предложению геттингенского физика Листинга (1808— 1882), принято называть геоидом.

Над способами перехода от поверхности эллипсоида к плоскости работали многие ученые, так как эта математическая задача может решаться по-разному в зависимости от выбранной картографической проекции.

Для построения картографического изображения значительной по площади территории, шарообразностью которой уже пренебречь нельзя, необходимо поверхность земного эллипсоида развернуть на плоскость. Однако этого нельзя сделать без того, чтобы картографическое изображение не испытало деформации (появления разрывов и складок), которая приводит к определенным искажениям углов, длин линий и площадей по сравнению с действительными расстояниями и направлениями на земном шаре. Все же эти искажения могут быть определены и учтены в процессе работы с картой. Процесс деформации можно себе представить, если изображенный рисунок на глобусе мысленно разрезать, вытянуть и совместить с плоскостью (рис. 3).

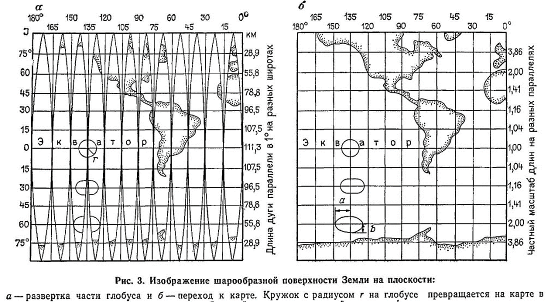
В настоящее время переход от эллипсоида к плоскости выражается уравнениями, определяющими аналитическую зависимость между прямоугольными координатами точек на плоскости (карте) и географическими координатами соответствующих точек на эллипсоиде.

Для построения топографических карт в социалистических странах применяется равноугольная проекция (не искажает углы, вследствие чего сохраняет подобие фигур, но искажает площади и длины линий), предложенная знаменитым математиком и астрономом Карлом Фридрихом Гауссом (1777—1855). Эта проекция была детально разработана в 1912 г. проф. Потсдамского геодезического института Л. Крюгером, который определил формулы непосредственного перехода от эллипсоида к плоскости. Эта система координат, получившая название «Гаусса — Крюгера», полностью отвечает вышеуказанным требованиям.

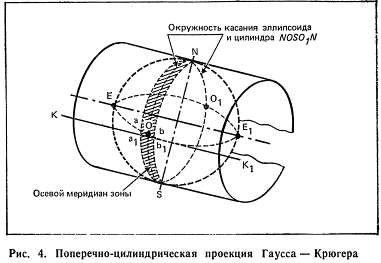
Поперечно-цилиндрическая проекция Гаусса — Крюгера (рис. 4) заключается в том, чтобы развернуть в плоскость узкие полосы (зоны) земного эллипсоида во избежание ощутимых искажений за счет сферичности Земли.

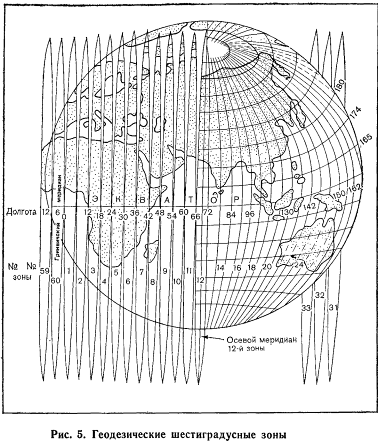
Это достигается путем разбивки поверхности эллипсоида меридианами на 60 зон (двуугольников) протяженностью каждая 6° по долготе (рис. 5). Нумерация зон ведется от Гринвичского меридиана (нулевого) на восток. В пределах зоны только осевой меридиан и отрезок экватора изображаются прямыми взаимно перпендикулярными линиями, а все остальные меридианы и параллели — кривыми.

Чем больше меридианы зон удалены от линии касания, тем больше искажения: этим и объясняется выбор узкой шестиградусной полосы (зоны), которая обеспечивает незначительные искажения. Каждая зона проектируется на один цилиндр, а шар поворачивается в нем, чтобы линии касания цилиндров совпадали со средними меридианами каждой из 60 зон, называемых осевыми меридианами зон.

Линия касания является общей для цилиндра и эллипсоида, и при переходе на боковую поверхность цилиндра длина меридиана касания не изменяется. Цилиндр, ось которого лежит в плоскости экватора эллипсоида 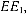своей боковой поверхностью касается среднего меридиана одной из 60 зон (см. рис. 4). Затем боковые поверхности цилиндров развертываются на плоскости, и получаются плоские изображения части сферической поверхности (шестиградусных зон), построенные в картографической проекции Гаусса — Крюгера.

Топографическая карта, отображающая территорию в пределах сферической зоны в картографической проекции Гаусса — Крюгера, практически не имеет искажений, и по ней можно получить истинные размеры расстояний, площадей, направлений.

В каждой из 60 зон строится самостоятельная система прямоугольных координат. Началом координат служит пересечение среднего меридиана зоны — оси абсцисс X с линией экватора — осью ординат У.

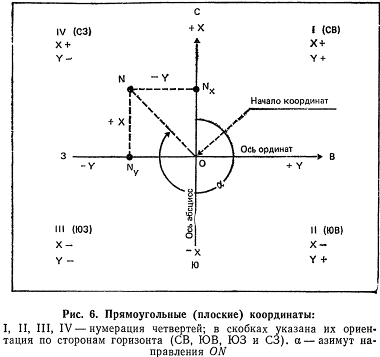
Расстояния от экватора (абсциссы при расположении в Северном полушарии) имеют положительный знак, но ординаты могут в пределах зоны различаться по знаку в зависимости от положения точки по отношению к осевому меридиану зоны: в восточной половине каждой зоны они будут положительными, в западной — отрицательными (рис. 6).

Для упрощения вычисления и избежание ошибок целесообразно иметь только положительные значения ординат, которые бы выражались одинаковым количеством цифр. Для этого достаточно увеличить каждую из них на 500 км, что достигается условным смещением оси X и соответственно начала координат На 500 км влево. Следовательно, все ординаты к востоку от осевого меридиана могут иметь значение от 500 до 833 км, а к западу— от 167 до 500 км.

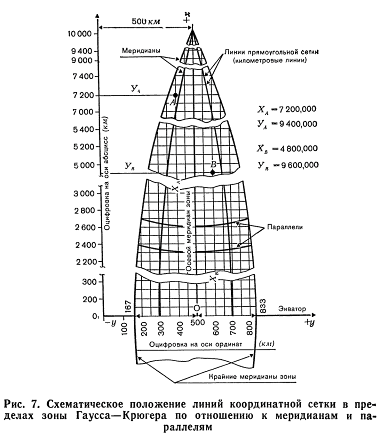
Положительное число 500 км выбрано по соображениям, что длина дуги в один градус по экватору равна округленно 111 км, следовательно, длина дуги в 3° составляет 333 км (рис. 7). Поэтому ординаты У в пределах зоны у точек пересечения экватора с крайними меридианами зоны могут иметь значения от —333 до +333 км. Прибавив к каждому из этих чисел +500 км, получим соответственно 167 и 833 км — положительные трехзначные числа.

Для того чтобы не принять точку одной зоны за точку другой, перед числом, обозначающим ординату У, пишут номер зоны, т. е. перед значением ординаты могут стоять цифры от 1 до 60. Чтобы узнать номер зоны, достаточно перенести запятую на три знака влево. Оставшиеся цифры укажут номер зоны. Например: Y= =36 725,321 читается: 36 зона, У=725,321 км.