Методы исследования поведения КА при динамических воздействиях

Расчет динамики всего космического комплекса проводится на самых ранних стадиях проектирования и уточняется при внесении существенных изменений в конструкцию КА в ходе конструирования. Для расчета динамики КА используется ряд математических методов исследования.

В общем случае реакция любой сложной механической системы на внешние или внутренние возмущения может определяться двумя путями — исследованием динамических процессов во временной или частотной области.

При изучении динамических процессов более предпочтительными являются исследования процессов в КА во временной области, так как они позволяют учитывать фазовые соотношения между составляющими процесс гармониками, которые во многом определяют максимальные мгновенные значения тонов колебаний. Количество их обычно не превышает 2—3. Исследование динамических процессов дает возможность подбора жесткостных характеристик конструкции КА в зависимости от параметров динамической схемы космического комплекса.

Для моделирования переходных процессов во временной области наиболее часто используются следующие модели: с распределенными или сосредоточенными параметрами, а также смешанные или конечно-разностные.

Распределенная модель имитирует реальную конструкцию в виде ограниченного (конечного) числа непрерывных элементов, каждый из которых описывается точным уравнением движения и граничными условиями. Основное достоинство распределенной модели — наиболее адекватное представление рассматриваемой конструкции, но это приводит к достаточно сложным системам уравнений, при которых проявляются трудности вычислительного характера.

В смешанных или комбинированных моделях континуальные элементы (стержни, оболочки) сочетаются с сосредоточенными инерционными элементами. При этом основной вклад в распределение жесткостей вносят континуальные элементы, а сосредоточенные элементы определяют инерционные характеристики.

Конечно-разностные модели получили распространение в расчетной практике только в последнее время, так как для их реализации применительно к сложным многорезонансным конструкциям требуются мощные ЭВМ. Конечно-разностные модели представляют исследуемую конструкцию в виде большого числа безмассовых жестких элементов со связями, сосредоточенными на общих границах, и массами, сконцентрированными в узловых точках.

К недостаткам этих моделей можно отнести:
- трудность выбора конечного элемента, удовлетворительно описывающего все составные части конструкции;
- большое время счета на ЭВМ нестационарной задачи динамики;
- ориентированность на решение линейных систем.

Модель с сосредоточенными параметрами (рис. 1.10) состоит из ограниченного числа масс и упругодиссипативных связей, приближенно представляющих конструкцию.

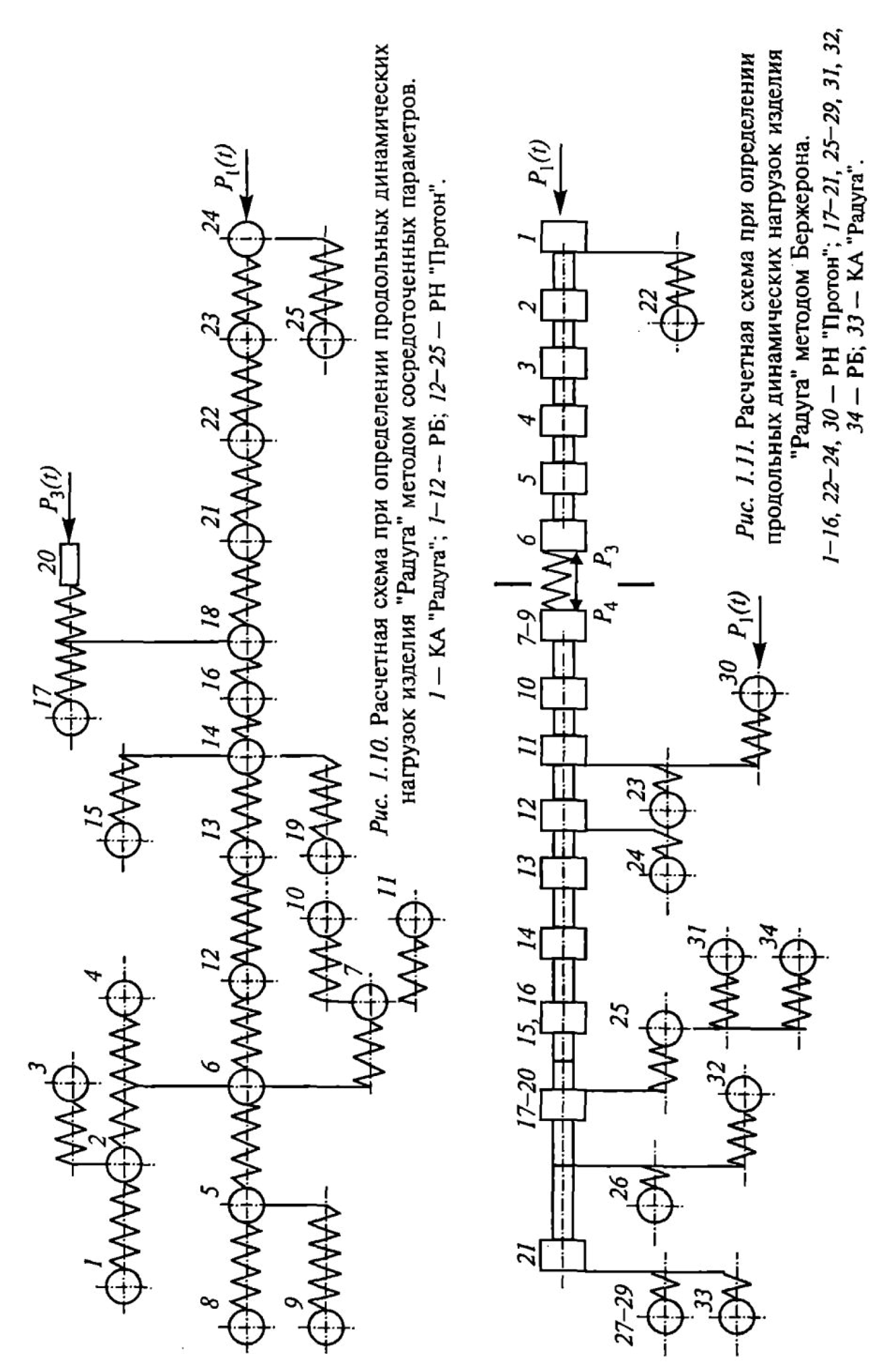
Модели дискретного типа получили широкое распространение при расчетах динамических характеристик конструкций, работающих в условиях нестационарного нагружения. Это объясняется наличием надежных алгоритмов и программ, обеспечивающих решение на ЭВМ систем обыкновенных дифференциальных уравнений при любых, в том числе и нестационарных, возмущениях, большей скоростью решения систем уравнений по сравнению с системами дифференциальных уравнений в частных производных, простотой введения нелинейности между элементами. Недостатки модели связаны с априорностью определения степени дискретизации и систем связей.

Выбор динамической модели, т.е. составление системы уравнений, описывающей условия динамического равновесия конструкции при приложенных внешних динамических силах, является наиболее сложной и ответственной задачей исследования динамики КА. Она должна правильно отражать основные свойства реальной системы и по возможности быть достаточно простой. Задача решается введением ряда ограничений и упрощений. Основным упрощением является приведение реальной системы с бесконечным числом степеней свободы, описываемой дифференциальными уравнениями в частных производных, к системе с ограниченным числом степеней свободы, движение которой может быть представлено конечным числом обыкновенных дифференциальных уравнений. Число степеней эквивалентной системы определяется выбранным числом сосредоточенных масс, количество последних выбирается в каждом конкретном случае в зависимости от условий нагружения, динамических характеристик системы и потребностей точности расчетов.

Анализ существующих моделей показывает, что наиболее применимыми для расчетов динамических процессов в изделиях РКТ являются смешанные модели и модели с сосредоточенными параметрами.

Задача представления реальной механической системы в виде смешанной (рис. 1.11) и сосредоточенной (см. рис. 1.10) моделей достаточно подробно рассмотрена в [1,4, 6, 22].

В работе изучена допустимость замены распределенной динамической модели корпуса термоконтейнера КА дискретной с сосредоточенными массами и жесткостями. Оценка точности такого представления определяется сравнением собственных частот распределенной и дискретной моделей.

Для прямого стержня постоянного сечения со свободными концами собственные частоты определяются по формуле

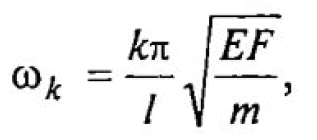
где Е— модуль продольной упругости; F— площадь поперечного сечения стержня; т — погонная масса стержня; / — длина стержня; к — номер частоты собственных колебаний.

Соотношение первых пяти собственных частот дискретной и распределенной моделей стержня приведено в табл. 1.2.

Для дискретных моделей массы участков стержня предполагались находящимися в центре участка.

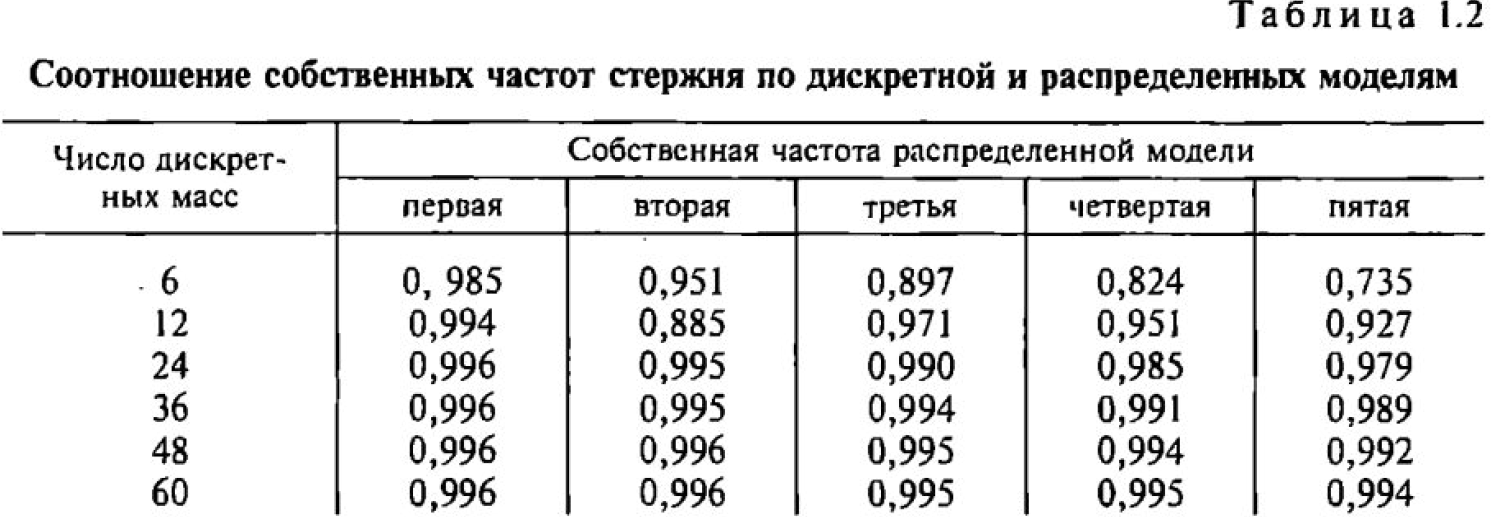
Анализ зависимости результатов вычисления частот дискретной модели от числа дискретных масс показывает, что с практической точки зрения точность вычисления первого тона колебаний удовлетворяет необходимой уже при представлении стержня шестью массами, а пятого — двадцатью четырьмя массами. Учитывая, что энергия колебаний сосредоточена в небольшом числе первых собственных тонов, можно утверждать о наличии некоторого предела увеличения числа масс (в данном случае — 48), выше которого рост точности практически отсутствует, а объем вычислений резко возрастает.

Из результатов, приведенных в табл. 1.2, можно сделать два основных вывода, в дальнейшем определяющих выбор для расчетов:
- для рассматриваемых механических систем модели с сосредоточенными параметрами позволяют проводить расчеты с достаточной точностью;
- при представлении реальной конструкции в виде дискретной модели нет необходимости чрезмерно ее усложнять разбиением на большое число элементов.

Для сравнения расчета реакций элементов совместной модели «РН+РБ+КА» можно подробно рассмотреть метод расчета модели с сосредоточенными параметрами и два метода расчета смешанных моделей.