Рычаги и клинья. Наклонные плоскости и клинья

Современный человек окружен самыми разнообразными машинами-от часов, стиральных машин и другой бытовой техники до компьютеров, летательных аппаратов, в том числе космических ракет. Все машины-в известном смысле механизмы, «экономящие труд», т.е. обеспечивающие механический выигрыш. Механический выигрыш машины можно оценить как отношение груза к усилию. Простейшие механизмы - рычаги, клинья и винты-тысячами используются во многих сложных машинах.

Выигрыш в силе. Рычаги встречаются на каждом шагу: лом, весло, отвертка, ножницы, качели и тачка-все это рычаги разного рода [1]. Они позволяют осуществить передвижение грузов с наименьшими усилиями. Механический выигрыш при использовании рычага определяется величинами груза и усилия, а также их расстояниями от точки опоры. Может ли четырехлетний ребенок поднять мужчину, весящего 75 кг? Может, если обоих посадить на качели — доску с опорой посередине. Если мужчина сядет достаточно близко к точке опоры, то массы ребенка окажется достаточно, чтобы его поднять (при условии, что ребенок будет сидеть на дальнем противоположном конце доски). При этом ребенок опустится ниже, чем мужчина поднимется вверх. Это неравенство смещений и будет компенсацией за возможность поднять большой груз малым усилием. Но большой груз все-таки поднимется-недаром греческий математик Архимед (287-212 гг. до н.э.) сказал: «Дайте мне точку опоры, и я переверну весь мир».

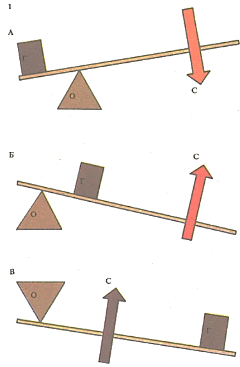
Рычаги разделяют на три рода в зависимости от взаимного положения приложенной силы С, груза Г и точки опоры О. Доска-качели - рычаг первого рода: точка опоры находится между грузом и приложенной силой (А). В рычагах второго рода [Б] сила поднимает груз, находящийся между точкой приложения усилия и точкой опоры. Так действуют тачки. В рычагах третьего рода (В) сила приложена} между грузом и точкой опоры. Таковы многие гидравлически управляемые устройства. И человек, и любая сложная машина не что иное, как система рычагов всех трех родов.

Уравновешенная доска-качели, как и любой рычаг, в котором масса поднимаемого груза и усилие сбалансированы, находится в равновесии. В положениях равновесия произведение массы груза на его горизонтальное расстояние до точки опоры равно произведению усилия на расстояние от точки приложения усилия до точки опоры. Если ребенок, весящий 12,5 кг, сидит на расстоянии 3 м от точки опоры, то он может сбалансировать мужчину массой 75 кг, сидящего на расстоянии 0,5 м от точки опоры на другом конце доски (12,5 x 3 = 75 x 0,5 = 37,5). В приведенном примере выигрыш в силе (отношение пропорционального массе груза к усилию) 75 :12,5 равен 6. Этот же выигрыш можно вычислить как отношение расстояния от точки приложения усилия до точки опоры к расстоянию груза от точки опоры (3 :0,5 = 6).

Произведение веса груза на расстояние до точки опоры называют моментом силы (груз выражается в единицах силы). В условиях равновесия момент веса груза равен моменту приложенного усилия. Если один из них больше другого, то появляется опрокидывающая сила и плечо с большим моментом будет опускаться.

Наклонные плоскости и клинья. Люди бронзового века, воздвигавшие Стоунхендж, как и древние египтяне, сооружавшие пирамиды, должны были поднимать колоссальные глыбы на высоту нескольких метров. Они уже знали, что гораздо легче толкать тяжелый груз вверх по наклонной плоскости, чем поднимать его вертикально вверх, поэтому они, вероятно, предварительно делали длинные наклонные земляные насыпи, по которым и втаскивали каменные глыбы (скорее всего, уложив их на деревянные катки). Физики называют такую насыпь «наклонной плоскостью».

Чтобы поднять десятитонный блок по вертикали на 1 м, требуется усилие 98 кН. Усилие же, необходимое для того, чтобы втащить тот же блок вверх по наклонной плоскости с уклоном 1 :20, составит около 4,9 кН (если пренебречь трением). При этом груз должен пройти путь 20 м, т.е. как и для рычага существенный выигрыш в силе связан со значительным проигрышем в расстоянии. Выигрыш силы определяется отношением высоты подъема к длине наклонной плоскости. Длинные наклонные плоскости сейчас для компактности располагают спиралью [8].

Наклонная плоскость позволяет поднимать на большую высоту (или спускать с нее) тяжелые грузы. В многоэтажном гараже автомобили спускаются на улицу с большой высоты. Длинный пандус (наклонная плоскость) позволил бы осуществить спуск, но занял бы слишком много места. Поэтому пандус обвивают вокруг здания, и он становится похожим на гигантский винт

Если тяжелый блок нужно лишь приподнять (например, чтобы обвязать его тросом), то под него можно вколотить клин. Клин подобен двум наклонным плоскостям, сложенным вместе тыльными сторонами. По неподвижной наклонной плоскости груз двигают; когда же работают клином, наклонная плоскость проталкивается под груз, чтобы сдвинуть его. Расклинивание вызывает весьма значительные усилия. Топор, стамеска, плуг и пневматические отбойные молотки – клинья.

На мальтийских каменоломнях песчаник подпиливают и, вгоняя в пропил клинья, раскалывают его на блоки.

Винты-витые клинья. Нитка резьбы винта-это просто наклонная плоскость, навитая вокруг цилиндра [5]. Такие витки называются винтовой спиралью, геометрия которой была изучена примерно в 200 г. до н. э. древнегреческим математиком Аполлонием Пергским. Инструменты для нарезки резьбы изобрел Архимед; он же придумал водоподъемную машину, главную часть которой составлял «архимедов» винт.

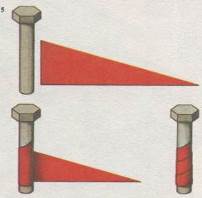
Винт можно представить как наклонную плоскость, навитую на цилиндр. Выигрыш в силе при наклонной плоскости (груз легче толкать по насыпи, чем поднимать вертикально) получается за счет вращения винта, развивающего значительные усилия. Шаг резьбы-не что иное, как расстояние, на которое смещается винт за один полный оборот.

Клин вбивают молотком, спиральный клин винта-ввинчиванием. Крутящий момент силы создается отверткой или гаечным ключом - рычагами. Следовательно, самый обыкновенный винт-это одновременно и рычаг, и клин, т. е. сложный механизм.

Расстояние между соседними витками резьбы, называемое шагом, служит мерой наклона соответствующей наклонной плоскости. За один полный оборот вокруг своей оси винт смещается на расстояние, равное одному шагу резьбы. Отношение длины рычага, поворачивающего винт, к величине шага резьбы характеризует выигрыш в силе. Коническая форма шурупа для дерева также ведет свое происхождение от клина (расклинивание способствует углублению шурупа в древесину). Углубляясь в мягкий металл, метчики-винты для нарезки-оставляют в металле винтовую нарезку.

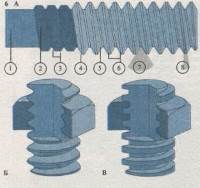
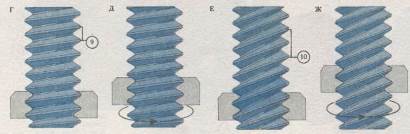
Винтовая резьба унифицирована и обычно описывается рядом специальных терминов. Различают [А] два диаметра: внутренний [1] и внешний [2]; толщиной резьбы [3] считают половину шага [6]. В нарезке различают нитку [4] и дно [5]. Свойства резьбы зависят также от угла профиля [7] и угла подъема резьбы [8]. Два основных типа резьбы подразделяются по профилю на круглую [Б] и квадратную [В]. В однозаходной резьбе [Г] единичный ход винта (9) и шаг резьбы равны. После полного поворота вокруг вертикальной оси [Д] гайка смещается на расстояние, равное шагу резьбы. В двухзаходной резьбе [Е] ход винта (10) соответствует удвоенному шагу резьбы и гайка смещается на два шага за один полный оборот винта [Ж].