Оценка соотношения «ёмкость-водоотдача»

Многие компьютерные модели были разработаны для расчета отношений «емкость-водоотдача», и они относительно легкодоступны. В этом разделе кратко описаны основные принципы, заложенные в основу этих моделей; более подробная информация приводится в разделах 4.2.4 и 4.2.5.

Численный метод. В своей основной форме оценка водоотдачи — это простое последовательное вычисление баланса между количеством воды, поступающей в водохранилище (сток, осадки), и сбрасываемой или потерянной водой из водохранилища (водозабор, испарение, утечка). Уравнение имеет следующий вид:

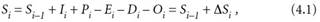
где S_i отображает запасы воды в водохранилище в конце временного интервала i, S_i-I отображает запасы в начале временного интервала i, Ii является притоком в течение интервала i, P_i является осадками в течение интервала i, E_i является испарением в течение интервала i, D_i является попуском или отведением во время интервала i, O_i является сбросом во время интервала i и ΔS_i. является изменением запасов воды в водохранилище в течение интервала i.

Там, где используется шаг по времени протяженностью в неделю или больше, средняя площадь поверхности водоема за интервал времени между t_i-I и t_i используется для расчета осадков и испарения.

Там, где водохранилище должно поддерживать определенный попуск, уравнение решается для различных предполагаемых максимальных емкостей (S) с целью найти итерационным способом объём, когда водохранилище почти истощается, или минимальный эксплуатационный объем.

Там, где уже существуют плотины или запасы воды постоянны, расход сбрасываемой воды, который должен поддерживаться, можно определить введением в уравнение вместо объёма воды в водохранилище объема попуска в качестве переменной. Последовательность значений ёмкости водохранилища, которая получается в результате решения уравнения, называется графиком изменения ёмкостей.

График, как правило, будет ограничен полным и минимальным эксплуатационным объемом водохранилища. В целом график для данной последовательности притока и нормы сброса будет функцией начальной емкости водохранилища и отличаться для разных начальных уровней. Однако, как только соответствующий полный или минимальный эксплуатационный объем будет достигнут, графики будут неразличимы для последовательности данных притока и нормы сброса.

Период максимальной сработки водохранилища, то есть от заполненного состояния до минимального эксплуатационного объема и восстановления снова до заполненного состояния, называют критическим периодом. Для достижения стабильности в анализе важно понимать, что критический период четко определяется с помощью графика изменения емкостей водохранилища.

Тем не менее, тщательный анализ графика в отношении возникновения периодов низкого потока остается очень важным. Потенциально более резкие периоды низкого стока по отношению к тем, что определяет критический период, могут наблюдаться в начале или в конце ряда значений притока, но только там, где первая или последняя часть таких периодов низкого потока может не входить в доступную длину ряда. Если есть такая вероятность, следует произвести приведение к норме сброса путём учёта фактического изменения запасов воды в водохранилище за период анализируемой последовательности данных.

В упрощенном случае, описанном выше, предполагалось, что водоотдача равна норме сброса. Можно, однако, поставить задачу отвести больше или меньше воды, нежели водоотдача водохранилища или системы водных ресурсов. Значимость целевого попуска по отношению к характеристикам водоотдачи водной системы более подробно описана в разделе 4.2.4.

Графический метод. Графический метод предлагает простую альтернативу для визуального представления результатов последовательного решения уравнения (4.1).

При известных притоке I и попуске D объем воды в водохранилище S за время t математически выражается уравнением:

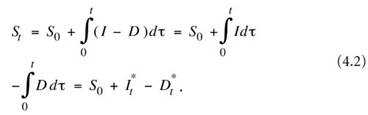
(Для удобства демонстрации влияние испарения и осадков исключено, и водозабор отображает весь отток воды. Потери будут там, где интегральная кривая оттока превышает интегральную кривую попуска, как это показано на рисунке II.4.4.).

Графики интегральных сумм I* и D* представляют собой соответственно интегральные кривые притока воды и оттока, а S_о является начальным объемом воды в водохранилище. Пример использования такого метода представлен на рисунке II.4.4, согласно которому полезный объем водохранилища S определен для постоянного попуска при условии, что водоснабжение будет бесперебойным в течение всего расчетного периода.

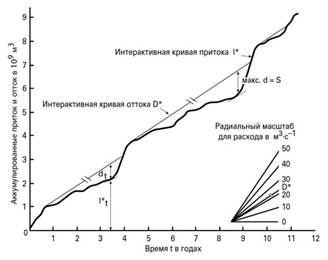
Рисунок II.4.4. метод массовой кривой для определения емкости водохранилища

Этот метод исходит из предположения полубесконечного (бездонного) водохранилища. Постоянный попуск соответствует постоянному наклону интегральной кривой D*. Линия, параллельная D*, проведена через каждый пик на интегральной кривой притока I*. Необходимый запас воды S равен максимальному вертикальному расстоянию между любой точкой на кривой I* и соответствующей ей точкой на любой из линий, параллельных D*.

Графический метод широко использовался в прошлом. Однако возможности компьютеров резко возросли за эти годы, что облегчает решение уравнения (4.1). Кроме того, цифровое решение обеспечивает большую гибкость при анализе различных сценариев, поэтому графический метод в настоящее время используется редко, если вообще используется.

Влияние длины ряда наблюдений. Хотя четких нормативов для минимальной длины ряда нет, надежный анализ водоотдачи, как правило, возможен при периоде наблюдений в 10-20 раз больше критического периода. Там, где изменчивость стока мала и где присутствует необходимость в основном в сезонном регулировании (менее одного года), минимальная длина ряда от 10 до 20 лет является достаточной. Однако в полузасушливых и засушливых районах обычно требуется водохранилище на срок более года, так как часто наблюдаются критические периоды от 5 до 10 лет и дольше. В таких условиях лучше использовать длину ряда от 50 до 100 лет.

Даже там, где существуют достаточно длительные наблюдения за стоком, в будущем неизбежны более серьезные наводнения и засухи. Кроме того, практически наверняка последовательности значений стока, наблюденные в прошлом, никогда не будут в точности повторяться в будущем. Однако очевидно, что чем дольше период наблюдений, на основе которого строится последовательность притока, тем более надежными будут оценки предполагаемой водоотдачи на выходе.

Хотя исторические наблюдения являются единственной доступной фактической информацией, улучшенная оценка возможных экстремальных явлений может быть получена посредством стохастической генерации стока, как описано в разделе 4.2.2.6.